Notebook

Le Bloc Note pour dessiner avec ipycanvas¶

ipycanvas est une bibliothèque légère, rapide et stable exposant l' API Canvas du navigateur à IPython.

Ce module est développé par Martin RENOU ingénieur logiciel scientifique chez QuantStack...

Il vous permet de dessiner directement dans un notebook des primitives simples à partir de Python comme du texte, des lignes, des polygones, des arcs, des images, etc.

Cet ensemble d'outils simple vous permet de dessiner littéralement n'importe quoi !

Installation d'ipycanvas :¶

Le module est normalement déjà disponible sur le serveur jupyterhub il suffit donc d'importer les fonctionnalités de Canvas:

In [ ]:

from ipycanvas import Canvas

/!\ A faire avant pour fonctionner dans Carnet sur iPad :

Vérifier si le module ipycanvas n'est pas déjà installé :

%pip list

> Sinon il faut l'installer en faisant :
> ```python
%pip install ipycanvas

Après quoi, il faudra quitter ce notebook pour mieux le redémarrer dans Carnet afin de poursuivre...

Découverte de Canvas :¶

Les méthodes du module ipycanvas sont le reflet de celles de l'API Web Canvas dont vous pouvez trouver des tutoriels et de la documentation en suivant ce lien: https://developer.mozilla.org/en-US/docs/Web/API/Canvas_API

Il existe cependant quelques différences :

ces méthodes correspondent plus précisément à celles de l'API Web CanvasRenderingContext2D ;

ces méthodes sont écritent en snake_case au lieu de camelCase , ainsi par exemple, canvas.fillStyle = 'red' en JavaScript devient canvas.fill_style = 'red' en Python.

A faire vous même n°1 :

Dans la cellule de code suivante, finaliser la transcription en Python du code Javascript ci-dessous correspondant à l'exemple basique présenté sur la page de l'API Web CanvasRenderingContext2D et vérifier que cela produit bien le dessin attendu...

HTML :

<canvas id="my-house" width="300" height="300"></canvas>

JavaScript :

const canvas = document.getElementById('my-house');
const ctx = canvas.getContext('2d');

// Set line width
ctx.lineWidth = 10;

// Wall
ctx.strokeRect(75, 140, 150, 110);

// Door
ctx.fillRect(130, 190, 40, 60);

// Roof
ctx.beginPath();
ctx.moveTo(50, 140);
ctx.lineTo(150, 60);
ctx.lineTo(250, 140);
ctx.closePath();
ctx.stroke();

In [ ]:

# Import module
from ipycanvas import Canvas

# Instance
ctx = Canvas(width=300, height=300)

# Set line width
ctx.line_width = 10

# Wall
ctx.stroke_rect(75, 140, 150, 110)

# Door
ctx.fill_rect(130, 190, 40, 60)

// Roof
ctx.beginPath();
ctx.moveTo(50, 140);
ctx.lineTo(150, 60);
ctx.lineTo(250, 140);
ctx.closePath();
ctx.stroke();

# Display
ctx

Dessins de primitives simples :¶

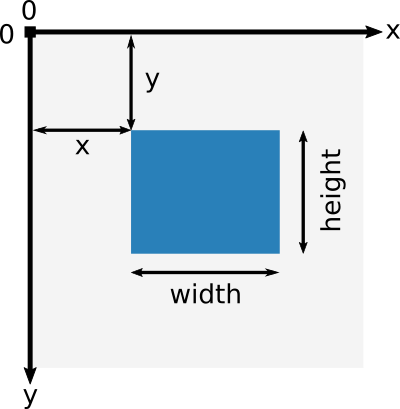
Avant de pouvoir commencer à dessiner, nous devons parler de la grille du canevas.

L'origine de cette grille est positionnée dans le coin supérieur gauche à la coordonnée (0,0).

Tous les éléments sont placés par rapport à cette origine.

Ainsi, la position du coin supérieur gauche du carré bleu devient x pixels à partir de la gauche et y pixels à partir du haut, aux coordonnées (x, y).

Le répérage est donc un peu différent de celui que vous avez pratiqué en Mathématiques, il faudra s'adapter et aborder les choses sous un autre angle...

Tant mieux, car c'est l'occasion de sortir de sa zone de confort pour certains, ou d'inconfort pour d'autres, afin de mieux (ré)apprendre les notions utiles à l'éxécution d'un dessin sur une machine numérique.

Dessiner des rectangles :¶

Il existe deux méthodes pour dessiner un rectangle sur le canevas :

fill_rect(x, y, width, height=None): Dessine un rectangle plein. Si height est homis, il est défini sur la même valeur que width.
stroke_rect(x, y, width, height=None): Dessine un contour rectangulaire. Si height est homis, il est défini sur la même valeur que width.

Vous pouvez également effacer une certaine zone de rectangle de canevas:

clear_rect(x, y, width, height=None): Efface la zone rectangulaire spécifiée, la rendant totalement transparente. Si heightest homis, il est défini sur la même valeur que width.

A faire vous même n°2 :

Exécuter progressivement les instructions des cellules suivantes ;
Ajouter des commentaires pour décrire ce que produisent chacune de ces instructions ;
Amusez vous à changer l'ordre d'exécution des cellules...

In [ ]:

from ipycanvas import Canvas

In [ ]:

cr = Canvas(width = 200, height = 160)

In [ ]:

cr

In [ ]:

cr.fill_style = 'rgb(220, 220, 220)'
cr.fill_rect(0, 0, 200, 160)

In [ ]:

cr.fill_style = "yellow" 
cr.fill_rect(25, 40, 150, 80)

In [ ]:

cr.stroke_style = '#FF0000'
cr.stroke_rect(25, 40, 150, 80)

In [ ]:

cr.clear_rect(70, 50, 60)

In [ ]:

cr.clear()

A faire vous même n°3 :

Que permet la fonction clear() ?

...

Considérant que le gris correspond à l'image d'un fond (background) il aurait été intéressant de pouvoir effacer le jaune sans traverser tout l'arrière plan. Non verrons plus tard qu'ipycanvas propose des solutions évoluées pour éviter cela, mais à ce stade, que proposeriez vous de faire pour ça :

...

En vous inspirant du code de l'exemple basique du "A faire vous même n°1", ajouter une instruction qui permette d'épaissir le cadre rouge du rectangle dessiné en bordure...

In [ ]:

Les couleurs¶

Le Canvas a deux attributs de couleur, un pour les traits et un pour les surfaces. Vous pouvez également modifier la transparence globale.

stroke_style: (couleur HTML valide) La couleur des rectangles et des tracés. La valeur par défaut est "black" ;

fill_style: (couleur HTML valide) La couleur de remplissage des rectangles et des chemins. La valeur par défaut est "black" ;

global_alpha: (float) Niveau de transparence. Par défaut à 1.0.

couleur HTML valide est une chaine de caractère (type str) telle que 'rgb(220, 220, 220)', "yellow", '#FF0000', "rgba(0, 0, 255, 0.5)", ...

Pour plus d'information à ce sujet : https://www.w3schools.com/colors/colors_picker.asp

A faire vous même n°4 :

Produire un code qui dessine le drapeu Français ;

In [ ]:

from ipycanvas import Canvas
dfr = Canvas(width = 200, height = 140)
dfr

In [ ]:

# A compléter

Dessiner des cercles :¶

Il existe deux méthodes pour dessiner un cercle (ou plus exactement un arc de cercle refermé) sur le canevas :

fill_arc(x, y, radius, start_angle, end_angle, anticlockwise=False) : Dessine un arc plein fermé centré sur (x, y) avec un rayon radius, la forme dessinée se situe entre start_angle et end_angle en radians, du coté d'un parcours dans le sens des aiguilles d'une montre par défaut anticlockwise=False ;
stroke_arc(x, y, radius, start_angle, end_angle, anticlockwise=False): Dessine un contour d'arc fermé centré sur (x, y) avec un rayon radius, la forme dessinée se situe entre start_angle et end_angle en radians, du coté d'un parcours dans le sens des aiguilles d'une montre par défaut anticlockwise=False ;

Ici encore, à l'inverse du sens trigonométrique tel que vu en Mathématiques, les angles sont orientés positivement dans le sens des aiguilles d'une montre.

Aussi, nous utiliserons les propriétés trigonométriques du triangle de Pythagore, avec l'hypoténuse égale au rayon radius de notre arc de cercle : $$rayon * sin(angle) = opposé$$$$rayon * cos(angle) = adjacent$$

A faire vous même n°5 :

Exécuter progressivement les instructions des cellules suivantes ;
Ajouter des commentaires pour décrire ce que produisent chacune de ces instructions ;
Remplacer les couleurs rouge, verte et bleue par du jaune, cyan et magenta...

In [ ]:

from ipycanvas import Canvas

In [ ]:

from math import pi, sin, cos

In [ ]:

cc = Canvas(width = 200, height = 200 + 2)

In [ ]:

cc

In [ ]:

cc.line_width = 2

In [ ]:

cc.stroke_style = 'red'
cc.stroke_arc(100 - 50 * cos(pi/6), 100 - 50 * sin(pi/6), 50, - pi/6, pi/2, True)

In [ ]:

cc.stroke_style = 'green'
cc.stroke_arc(100 + 50 * cos(pi/6), 100 - 50 * sin(pi/6), 50, pi/2, 7*pi/6, True)

In [ ]:

cc.stroke_style = 'blue'
cc.stroke_arc(100, 100 + 50, 50, - pi/6, 7*pi/6, False)

In [ ]:

cc.fill_style = "rgba(255, 0, 0, 0.3)"
cc.fill_arc(100 - 50 * cos(pi/6), 100 - 50 * sin(pi/6), 50, 0, 2*pi)

In [ ]:

cc.fill_style = "rgba(0, 255, 0, 0.3)"
cc.fill_arc(100 + 50 * cos(pi/6), 100 - 50 * sin(pi/6), 50, 0, 2*pi)

In [ ]:

cc.fill_style = "rgba(0, 0, 255, 0.3)"
cc.fill_arc(100, 100 + 50, 50, 0, 2*pi)

A faire vous même n°6 :

Produire un code qui dessine le drapeau du Bangladesh ;

In [ ]:

from ipycanvas import Canvas
dba = Canvas(width = 200, height = 140)
dba

In [ ]:

# A compléter

Des dessins paramétrés :¶

Nous allons utiliser des variables pour paramétrer notre code ce qui va nous permettre par la suite de faire évoluer le dessin produit très simplement.

A faire vous même n°7 :

Dans la cellule de code suivante, finaliser le paramétrage de l'exemple du A faire vous même n°5 en utilisant les variables rayon et largeur et vérifier qu'il produit la même figure que précédemment ;
Ensuite, modifier seulement la valeur de la variable epaisseur, quel effet cela produit ?

...

Proposer alors un autre nom pour cette variable : ...

In [ ]:

from ipycanvas import Canvas
from math import pi, sin, cos

# Variables pour le paramétrage 
epaisseur = 2 # valeur entière de 1 à 9
rayon = epaisseur * 25
largeur = rayon * 2

# Finir le paramétrage du code avec les variables rayon et largeur et le commenter
cc = Canvas(width = 200, height = 200 + epaisseur)

# Paramétrage de l'épaisseur des traits
cc.line_width = epaisseur

cc.stroke_style = 'red'
cc.stroke_arc(100 - 50 * cos(pi/6), 100 - 50 * sin(pi/6), 50, - pi/6, pi/2, True)

cc.stroke_style = 'green'
cc.stroke_arc(100 + 50 * cos(pi/6), 100 - 50 * sin(pi/6), 50, pi/2, 7*pi/6, True)

cc.stroke_style = 'blue'
cc.stroke_arc(100, 100 + 50, 50, - pi/6, 7*pi/6, False)

cc.fill_style = "rgba(255, 0, 0, 0.3)"
cc.fill_arc(100 - 50 * cos(pi/6), 100 - 50 * sin(pi/6), 50, 0, 2*pi)

cc.fill_style = "rgba(0, 255, 0, 0.3)"
cc.fill_arc(100 + 50 * cos(pi/6), 100 - 50 * sin(pi/6), 50, 0, 2*pi)

cc.fill_style = "rgba(0, 0, 255, 0.3)"
cc.fill_arc(100, 100+50, 50, 0, 2*pi)

# Affichage du canvas
cc

A faire vous même n°8 :

Dans la cellule suivante, reprendre le code correspondant au drapeau du Bangladesh et le paramétrer pour qu'il produise aussi les drapeaux des Palaos ou du Japon en ne changeant que les valeurs de quelques variables ;

In [ ]:

# A compléter

A ce stade, on analyse qu'il serait intéressant de pouvoir regrouper plusieurs informations variables simples dans une seule variable. Plusieurs structures sont envisageables alors pour organiser ces données élémentaires en variable ainsi construite :

une variable pays pour chaque pays informations élémentaires le concernant... ;
une variable couleurs_fond qui regrouperait toutes les valeurs de couleur_fond selon les pays, et de même avec couleurs_disque et positions_disque ;

On peut même envisager une structure plus globale qui regrouperait toutes ces informations...

Un question se pose alors, comment va-t'on extraire chaque information élémentaire d'une telle structure ?

Un peu d'interactivité avec ipywidgets :¶

Jupyter dispose d'un module pour afficher dans un notebook des éléments HTML de dialogue comme des boutons ou des slider afin de permettre à l'utilisateur d'interagir avec le code via cette interface homme machine (IHM). Il s'agit d'ipywidgets.

Il est donc possible d'installer un dialogue entre l'utilisateur et le dessin que produit ipycanvas grace à ipywidgets.

Nous ne ferons ici qu'une rapide introduction afin de comprendre le principe du fonctionnement et de découvrir les éléments qui sont nécessaires pour la mise en place de cette interractivité.

A faire vous même n°9 :

Exécuter la cellule de code suivante, qui contient un exemple proposé par Martin RENOU afin de déplacer la balle dans le canvas grace à deux sliders...

In [ ]:

# Code exemple proposé par Martin RENOU développeur d'ipycanvas 
from math import pi

from ipywidgets import IntSlider, VBox
from ipycanvas import Canvas, hold_canvas

# Create x and y sliders, which will control the ball position
x_slider = IntSlider(description='x:', min=0, max=300, value=150)
y_slider = IntSlider(description='y:', min=0, max=300, value=150)

canvas = Canvas(width=300, height=300)

# Function that will clear the canvas and redraw the ball
def redraw_circle(x, y):
    with hold_canvas(canvas):
        canvas.clear()
        
        ### C'est dans cette zone de la fonction redraw_circle() qu'il y a l'instruction du dessin
        
        canvas.fill_arc(x, y, 20, 0, 2 * pi)
        
        ###
        

# Observe sliders changes, and call redraw_circle whenever the sliders change
x_slider.observe(lambda _: redraw_circle(x_slider.value, y_slider.value))
y_slider.observe(lambda _: redraw_circle(x_slider.value, y_slider.value))

# Initial draw
redraw_circle(x_slider.value, y_slider.value)

display(x_slider)
display(y_slider)
display(canvas)

A faire vous même n°10 :

Dans la cellule suivante, coller les instructions du dessin de la figure paramétrée de l'activité n°7 afin de piloter l'échelle du dessin avec un slider et vérifier le bon fonctionnement...

In [ ]:

from math import pi, sin, cos
from ipywidgets import IntSlider, VBox
from ipycanvas import Canvas, hold_canvas

# Création d'un slider pour controler le facteur d'échelle défini par l'épaisseur des traits de la figure
e_slider = IntSlider(description='épaisseur :', min=1, max=9, value=2)

# Création d'un canvas support pour notre dessin
cc = Canvas(width = 100 * e_slider.max, height = 101 * e_slider.max)

# Fonction pour effacer le canvas et y redessiner la figure
def figure(epaisseur):
    with hold_canvas(cc):
        cc.clear()
        
        # Variables pour le paramétrage       
        rayon = epaisseur * 25
        largeur = rayon * 4 
               
        #### Coller dans cette zone de la fonction l'ensemble des instructions de dessin de la figure paramétrée                        

        ###
        
# Cette fonction observe à chaque instant l'état du slider et en cas de changement elle rappelle la fonction figure()
e_slider.observe(lambda _: figure(e_slider.value))

# Premier appel à la fonction figure() pour produire le dessin initial
figure(e_slider.value)

# Affichage du slider et du canvas
display(e_slider)
display(cc)

Nous reviendrons donc plus tard et plus avant sur la programmation d'une IHM telle que celle d'ipywidgets, ce qu'il faut comprendre et retenir à ce stade c'est que pour installer l'interactivité il est essentiel de paramétrer le code avec des variables et de le structurer dans des fonctions...

Un point fait tout !¶

Une image matricielle étant constituée de pixels (picture elements), nous devrions pouvoir, à l'instar du Pointillisme, en défininissant une fonction personalisée point() et à l'aide de boucles et de tests conditionnels, écrire des scripts pour dessiner des images géométriques.

Aussi, en y ajoutant un peu de pseudo-aléatoire nous pourrions écrire et même partager des programmes qui produisent de l'Art génératif...

Premières fonctions personalisées :¶

A faire vous même n°11 :

Exécuter la cellule suivante qui dessine dans un canvas nommé toile un arrière plan de couleur linen (blanc lin, #FAF0E6) et définit une fonction point(x, y, couleur, taille) qui dessine un dique de couleur couleur, de rayon taille, et dont le centre a pour coordonnés x et y;
Essayer plusieurs fois d'appeler la fonction point(x, y, couleur, taille) en lui passant différentes valeurs...
A la lecture de la dernière documentation d'ipycanvas, proposer une version plus simple pour réaliser la fonction point(x, y, couleur, taille)...

In [ ]:

from ipycanvas import Canvas
from math import pi, sin, cos

# Toile support du dessin
toile = Canvas(width = 200, height = 200)

# Background, l'arrière plan
toile.fill_style = 'linen'
toile.fill_rect(0, 0, toile.width, toile.height)

# Fonction point
def point(x, y, couleur, taille) :
    toile.fill_style = couleur
    toile.fill_arc(x, y, taille, 0, 2*pi)

toile    

In [ ]:

point(toile.width/2, toile.height/2, 'darkorange', 2)

In [ ]:

point(..., ..., ..., ...)

In [ ]:

# Fonction point() plus simple
def point(x, y, couleur, taille) :
    toile.fill_style = couleur
    # A compléter...

In [ ]:

point(..., ..., ..., ...)

In [ ]:

point(..., ..., ..., ...)

A faire vous même n°12 :

Modifier le script précédent pour définir une fonction background() qui applique la couleur_fond qui lui est passée en paramètre, sur toute la toile ;
Faire des appels successifs à votre fonction background() en lui passant différentes valeurs pour couleur_fond et en alternant avec des appels à la fonction point() ;
Quel effet cela produit ?

...

In [ ]:

# Fonction background à définir
def background(couleur_fond) :
    # A compléter...    
    
    

In [ ]:

toile

In [ ]:

background('snow')

In [ ]:

point(toile.width/2, toile.height/2, 'purple', 20)

In [ ]:

background(...)

Avec des boucles :¶

Pour automatiser des appels répétitifs aux fonctions point() et background(), on peut avantageusement les inscrire dans des boucles de répétition...

A faire vous même n°13 :

Exécuter les deux cellules suivantes ;
Commenter le code pour décrire ce que produisent chacun des blocs d'instructions de la seconde cellule ;
Décommenter l'instruction rayon = rayon + 1 et réexécuter cette cellule, puis décrire ce qu'il se passe alors :

...
Amusez-vous à modifier les valeurs des paramètres variables...

In [ ]:

# Code de définition d'un nouveau canvas
from ipycanvas import Canvas
from math import pi, sin, cos

# Toile support du dessin
toile = Canvas(width = 200, height = 200)

# Fonction point
def point(x, y, couleur, taille) :
    toile.fill_style = couleur
    toile.fill_arc(x, y, taille, 0, 2*pi)

toile 

In [ ]:

# Code applicatif
#
toile.clear()

#
n = 48
rayon = 12

#
for i in range(2*n) :
    point(toile.width/2 + rayon * cos(i * 2*pi/n), toile.height/2 - rayon * sin(i * 2*pi/n) , 'tomato', 2)
    # rayon = rayon + 1
    

A faire vous même n°14 :

Avec votre fonction background() et en appelant votre fonction point() dans une boucle, écrire les scripts pour reproduire les dessins de lignes suivantes :

Verticale	Diagonale 1	Diagonale 2

Pontillée	Parabolique	Sinusoïdale

Avec votre fonction background() et en utilisant votre fonction point() et des tests conditionnels dans une boucle écrire un script pour reproduire le dessin d'une ligne horizontale pointillée tricolore avec les couleurs du drapeau Français tel que :

In [ ]:

# Code de définition d'un nouveau canvas
from ipycanvas import Canvas
from math import pi, sin, cos

# Toile support du dessin
toile = Canvas(width = 300, height = 300)

# Fonction background()
def background(couleur_fond) :
    # A compléter...
    
    
# Fonction point()
def point(x, y, couleur, taille) :
    # A compléter...
    
    

# Affichage
toile    

In [ ]:

# Code applicatif  ligne verticale

In [ ]:

# Code applicatif  ligne diagonale 1

In [ ]:

# Code applicatif  ligne diagonale 2

In [ ]:

# Code applicatif ligne horizontale pointillée

In [ ]:

# Code applicatif ligne parabolique

In [ ]:

# Code applicatif ligne sinusoïdale

In [ ]:

# Code applicatif ligne horizontale tricolore

A faire vous même n°15 :

Programmer des scripts pour reproduire les drapeaux de la Finlande et de la Jamaïque...

Encore des boucles avec de l'aléatoire et un peu d'animation :¶

A faire vous même n°16 :

Coller dans la première cellule la définition de vos fonctions background(couleur_fond) et point(x, y, couleur, taille);
Exécuter les deux cellules suivantes ;
Commenter le code pour décrire ce que produisent chacun des blocs d'instructions de la seconde cellule ;
Décommenter les instructions background('black') et sleep(0.2), réexécuter cette cellule, puis décrire ce qu'il se passe alors :

...

Ajouter une condition pour que la fonction background('black') ne soit appelée qu'une fois tous les 15 tours de la boucle ;
Ajouter alors un choix aléatoire de la couleur couleur_fond sans transparence avant chaque rafraichissement de l'arrière plan ;
Amusez-vous à modifier d'autres paramètres et/ou ajouter d'autres fonctionnalités...

In [ ]:

# Code de définition d'un nouveau canvas
from ipycanvas import Canvas
from math import pi, sin, cos
from time import sleep

# Toile support du dessin
toile = Canvas(width = 200, height = 200)

# Fonction background()
def background(couleur_fond) :
    # A compléter...
    
# Fonction point()
def point(x, y, couleur, taille) :
    # A compléter...

toile

In [ ]:

# Code applicatif
#
toile.clear()

#
from random import choice, randint

#
for n in range(300) :
    #
    choix = "0123456789ABCDEF"
    couleur = "#"
    for k in range(8) :
        couleur += choice(choix)
    
    #
    x = randint(0, toile.width) #
    y = randint(0, toile.width) #
    taille = randint(10, 20) #
    
    # 
    # background('black')
    
    #
    point(x, y, couleur, taille)
    
    # 
    # sleep(0.2)

A faire vous même n°17 :

Avec votre fonction background() et en utilisant votre fonction point() et des tests conditionnels dans des boucles imbriquées, écrire un script pour reproduire une animation similaire à la vidéo ci-dessous :

In [ ]:

# Code de définition d'un nouveau canvas
from ipycanvas import Canvas
from math import pi, sin, cos
from time import sleep

# Toile support du dessin
toile = Canvas(width = 300, height = 200)

# Fonction background
def background(couleur_fond) :
    # A compléter...
    
# Fonction point
def point(x, y, couleur, taille) :
    # A compléter...
    
toile 

In [ ]:

# Code applicatif

Encore d'autres fonctions personnalisées à partager :¶

A faire vous même n°18 :

Dans la cellule suivante, ajouter votre fonction background(), et définir une fonction point_carre(x, y, couleur, taille) qui dessine un carré plein, de couleur couleur, de coté taille, et dont le centre a pour coordonnés x et y, et l'utiliser à la place de la fonction point() dans l'un ou l'autre des codes des activités précédentes...

/!\ Attention : Les coordonnées de la méthode fill_rect(x, y, width, height=None) sont définies dans le coin suppérieur gauche du rectangle or ici nous souhaitons que les coordonnées de la fonction point_carre(x, y, couleur, taille) soient définies au centre de la figure.

Les fonctions point() et point_carre() sont-elles transposables ?

...

Ne pas confondre point carré et Poincaré... ;)

In [ ]:

# Code de définition d'un nouveau canvas
from ipycanvas import Canvas
from math import pi, sin, cos
from time import sleep

# Toile support du dessin
toile = Canvas(width = 200, height = 200)
  
# Fonction background()
def background(couleur_fond) :
    # A compléter
    
# Fonction point()
def point(x, y, couleur, taille) :
    # A compléter...

# Fonction point_carre()
def point_carre(x, y, couleur, taille) :
    # A définir

toile 

In [ ]:

# Ajouter votre code applicatif à tester ci-dessous

#
toile.clear()

# ...

A faire vous même n°19 :

Ajouter la définition de votre fonctions point_carre() dans la cellule suivante de code de définition d'un nouveau canvas.
Définir une fonction cercle(x, y, couleur, taille, epaisseur) qui dessine le contour d'un cercle de couleur couleur, d'épaisseur de trait epaisseur, de rayon taille, et dont le centre a pour coordonnés x et y ;
Définir une fonction carre(x, y, couleur, taille, epaisseur) qui dessine le contour d'un carré de couleur couleur, d'épaisseur de trait epaisseur, de coté taille, et dont le centre a pour coordonnés x et y ;
Enregistrer tout le code de cette première cellule dans un nouveau fichier nommé mon_module_toile.py à placer dans le même dossier répertoire que ce notebook.
Exécuter le code de la seconde cellule suivante afin d'importer toutes les fonctions du fichier mon_module_toile.py dans l'environnement Python de ce notebook.
Tester vos fonctions avec le code applicatif proposé dans la troisième cellule suivante que vous commenterez...
Echanger votre fichier mon_module_toile.py avec celui de votre binôme, vos programmes sont-ils transposables ?

...

Soyez créatif, personnaliser votre travai en y ajoutant de nouvelles fonctionnalités...

In [ ]:

# Code de définition d'un nouveau canvas à enregistrer dans un fichier nommé mon_module_toile.py
from ipycanvas import Canvas
from math import pi, sin, cos


# Création d'une toile support pour le  dessin
toile = Canvas(width = int(input('Largeur en pixels ?')), height = int(input('Hauteur en pixels ?')))  
    
# Fonction point()
def point(x, y, couleur, taille) :
    # A compléter...

# Fonction point_carre()
def point_carre(x, y, couleur, taille) :
    # A définir
    
# Fonction cercle()
def cercle(x, y, couleur, taille, epaisseur) :
    # A définir
    
# Fonction carre()
def carre(x, y, couleur, taille, epaisseur) :
    # A définir

In [ ]:

from mon_module_toile import *
toile

In [ ]:

# code applicatif pour tester toutes les nouvelles fonctions du fichier mon_module_toile.py

#
toile.clear()

#
from random import choice, randint
from time import sleep

#
for n in range(300) :
    #
    choix = "0123456789ABCDEF"
    couleur = "#"
    for k in range(8) :
        couleur += choice(choix)
    
    #
    x = randint(0, toile.width) #
    y = randint(0, toile.height) #
    taille = randint(10, 20) #
    epaisseur = randint(1, 10) #
    
    # 
    if n % 4 == 0 :
        point(x, y, couleur, taille)
    elif n % 4 == 1 :
        carre(x, y, couleur, taille, epaisseur)
    elif n % 4 == 2 :
        cercle(x, y, couleur, taille, epaisseur)
    else :
        point_carre(x, y, couleur, taille)
    
    # 
    sleep(0.2)

Whaou, trop beau !

Le résultat vous satisfait ?

Si oui, faire un simple clic droit sur le canvas pour en télécharger un fichier image au format PNG.

Cool, trop fort !

En route vers la modularité :¶

Maintenant que vous avez écrit votre premier micro-module, un programme python qui regroupe toutes vos fonctions personnalisées destinées à un domaine d'application spécifique, pour permettre son partage et son réemploi futur par vous même ou tout autre utilisateur il va s'avérer utile de documenter votre code et en particulier de bien spécifier vos fonctions personalisées.

Par exemple regardons comment Martin RENOU a documenté le code du module ipycanvas en exécutant la cellule de code suivante :

In [ ]:

# Importation du module ipycanvas de Martin RENOU
from ipycanvas import Canvas

# Création d'un nouveau canvas pour l'exemple
bar = Canvas(width = 100, height = 100)

# Appel à l'aide...
help(bar.scale)

Vous saurez dorénavant qu'il existe une méthode scale() que vous pourrez bien appliquer à vos canvas en suivant son mode d'emploi indiqué dans cette documentation.

Observez aussi que, bien que Français, Martin a choisi l'Anglais pour documenter le code de son module...

Nous y reviendrons plus tard et de façon plus précise à l'occasion d'un notebook spécifique sur les fonctions et leur spécification.... Mais pour l'instant et à minima, il s'agit d'écrire une docstring, c'est à dire une chaine de caractères multignes inscrite entre deux triplets d'apostrophes ' (ou de guillements) " en entête de toutes vos fonctions tel que (tester les cellules de codes suivantes) :

In [ ]:

# Une fonction documentée mais qui ne fait rien, en fait, elle passe son tour...

def foo() :

    '''
    Ceci est une chaine de caractères multilignes

    Elle sert à documenter ma fonction pour des usages futures

    Je peux y mettre tout ce que je veux... Même de l'art ASCCI... Mais en responsabilité... 

    C'est ce texte qui s'affichera lors d'un appel à l'aide concernant ma fonction !

    '''
    pass

In [ ]:

foo()

In [ ]:

help(foo)

In [ ]:

? foo

Pourquoi les noms foo et bar ?

Voir aussi d'autres variables métasyntaxiques...

A faire vous même n°20 :

Prenez le temps de bien documenter vos fonctions...

Des chemins tout tracés :¶

Un chemin est une liste de points, reliés par des segments de lignes qui peuvent être de différentes formes, courbes ou non, de largeur et de couleur différentes. Un chemin peut resté ouvert ou être fermé.

Voici les étapes à programmer pour dessiner avec des chemins :

Tout d'abord, créer le chemin avec begin_path() ;
Ensuite, ajouter successivement toutes les commandes de dessin nécessaires pour définir le tracé à inclure dans le chemin telles que par exemple :
- move_to(x, y) : Déplace le crayon vers les coordonnées spécifiées par x et y ;
- line_to(x, y) : Ajoute une ligne droite au chemin actuel en connectant le dernier point du chemin aux coordonnées (x, y) spécifiées ;
- arc(x, y, radius, start_angle, end_angle, anticlockwise=False) : Crée un arc de cercle centré en (x, y) avec un rayon radius. Le chemin commence à start_angle et se termine end_angle en radians, et se déplace dans la direction donnée par anticlockwise qui par défaut est False donc dans le sens des aiguilles d'une montre ;
- rect(x, y, width, height) : Dessine un rectangle dont le coin supérieur gauche est spécifié par (x, y) de largeur width et de hauteur height;
- d'autres méthodes sont possibles : https://ipycanvas.readthedocs.io/en/latest/drawing_shapes.html#draw-commands
- l'instruction close_path() ajoute une ligne droite au chemin, allant au début du chemin actuel ;
Lorsque le chemin est défini, on peut faire dessiner le contour du tracé avec l'instruction stroke() et/ou peindre une forme pleine en remplissant la zone contenue dans le tracé avec l'instruction fill(rule).

A faire vous même n°21 :

Exécuter le code de la cellule suivante à plusieurs reprises tout en décommentant progressivement les instructions rendues inactives dans le script ;
Lorsque l'ensemble des instructions sont actives (décommentées) proposer un nom pour intituler le dessin produit : ... ;
Ajouter des commentaires pour définir ce que réalise chaque bloc d'instructions ;
Enfin, lorsque l'ensemble des instructions sont actives (décommentées) remplacer la valeur False de anticlockwise par un True, quel titre donner maintenant à ce dessin : ... ;
En maintenant la valeur de anticlockwise sur True, désactiver (commenter) à nouveau progressivement les instructions pour retrouver l'état initial du code mais pas celui du dessin...

In [ ]:

from ipycanvas import Canvas
from math import pi, sin, cos

#
canvas = Canvas(width=300, height=300)

#
# canvas.fill_style = 'green'
# canvas.fill_rect(0, 0, canvas.width, canvas.height)

#
canvas.begin_path()

#
# canvas.move_to(canvas.width/2, canvas.height/2)
canvas.arc(canvas.width/2, canvas.height/2, 100, -pi/6, pi/6, False)
# canvas.close_path()

#
# canvas.fill_style = 'orange'
# canvas.fill()

#
# canvas.line_width = 4
# canvas.stroke_style = 'purple'
canvas.stroke()

#
canvas

A faire vous même n°22 :

En employant les méthodes de tracés de chemins, représenter les anneaux olympiques tels que :

A faire vous même n°23 :

Soyez créatif pour imaginer un code qui dessine votre Avatar graphique pour GitHub et/ou Office365...

Références aux programmes :¶

Langages et programmation¶

Contenus	Capacités attendues	Commentaires
Constructions élémentaires.	Mettre en évidence un corpus de constructions élémentaires.	Séquences, affectation, conditionnelles, boucles bornées, boucles non bornées, appels de fonction.
Diversité et unité des langages de programmation.	Repérer, dans un nouveau langage de programmation, les traits communs et les traits particuliers à ce langage.	Les manières dont un même programme simple s’écrit dans différents langages sont comparées.
Spécification.	Prototyper une fonction. Décrire les préconditions sur les arguments. Décrire des postconditions sur les résultats.	Des assertions peuvent être utilisées pour garantir des préconditions ou des postconditions.
Utilisation de bibliothèques.	Utiliser la documentation d’une bibliothèque.	Aucune connaissance exhaustive d’une bibliothèque particulière n’est exigible.

Ressources :¶

Félicitations ! Vous êtes parvenu au bout des activités de ce bloc note.

Vous êtes maintenant capable de coder des scripts basés sur le module ipycanvas pour produire de superbes dessins dans l'environnement interactif jupyter notebook.

Aussi vous en savez suffisamment pour développer des mini-projets tels que Dessiner_ma_rue.ipynb, ou bientôt Let_it_snow.ipynb ou encore Coder_ma_carte_de_voeux.ipynb...

Pour explorer plus avant d'autres fonctionnalités de jupyter notebook repassez par le Sommaire.

Ce document original s'appuie sur le développement du module ipycanvas par Martin RENOU ingénieur logiciel scientifique chez QuantStack et est mis à disposition selon les termes de la Licence Creative Commons Attribution - Partage dans les Mêmes Conditions 4.0 International.

Pour toute question, suggestion ou commentaire : eric.madec@ecmorlaix.fr

In [ ]: