Logique Boléenne :¶

Un peu d'histoire :¶

En 1847, le Britanique George Boole développe un algèbre binaire pour traduire des raisonnements logiques sous forme d'équations dites booléennes.

En 1938, l'Américain Claude Shannon prouve que les circuits électriques peuvent résoudre tous les problèmes que l'algèbre de Boole peut résoudre.

Ceci et les travaux d'Alan Turing de 1936 constituent les fondements de l'informatique.

Algèbre de Boole :¶

Un booléen ne peut prendre que deux valeurs distinctes :

soit True = 1 (Vrai) ;
soit False = 0 (Faux).

On peut affecter un booléen à une variable. Il s'agit alors d'une variable binaire.

In [ ]:

continuer = True
type(continuer)

Les conditions, comparaisons et tests d'égalité, sont des expressions qui produisent un résultat booléen

In [ ]:

while continuer:              # la condition est vraie, on exécute le bloc de la boucle while
    print("demat")
    poursuivre = input("Voulez-vous continuer ? o/n : ")
    if poursuivre.lower() == 'n':
        print("kenavo")
        continuer = False     # la condition est fausse, on sort de la boucle

Les opérations fondamentales de l'algèbre de Boole sont :

la conjonction, ET, se note : and, $\&$ , $\bullet$, $∧$
la disjonction, OU, se note : or,$|$ , $+$, $∨$
la négation : NON, se note : not, $\bar{ }$, ~, $¬$

Avec ces opérateurs de base, nous allons pouvoir définir des fonctions logiques, exprimer des conditions qui combinent plusieurs tests.

In [ ]:

x = 5
if (x >= 0) and (x <= 10):
    print("Ce nombre appartient à l'intervalle [0 ; 10]")
else:
    print("Ce nombre n'appartient pas à l'intervalle [0 ; 10]")

Ici, les parenthèses permettent de mieux visualiser les tests.

L'algèbre de Boole répond à des règles, ainsi l’opérateur and est prioritaire sur l’opérateur or mais il vaut mieux utiliser des parenthèses pour plus de clarté : $ a + b \bullet c = a + (b \bullet c)$

Table de vérité :¶

Pour chaque fonction logique, on peut établir une table de vérité. Un tableau qui présente toutes les combinaisons de valeurs possibles pour une ou plusieurs variables, et la valeur associée de la fonction décrite. Le nombre de combinaisons est $2^n$ avec $n$ le nombre de variables booléennes combinées.

Fontion ET (AND):¶

La conjonction dont l'expression booléenne est a and b, est réalisée lorsque les conditions a et b sont toutes deux réalisées :

a	b	ET
0	0	0
0	1	0
1	0	0
1	1	1

Equation booléenne : $a \bullet b = a \& b = a ∧ b$

A faire vous-même :

Modifier le programme suivant pour obtenir une table de vérité avec le même ordre de combinaisons logiques que ci-dessus.

In [ ]:

# Table de vérité en Markdown par Python de l'opérateur ET :
from IPython.display import Markdown
    
table ='''|  a  |  b  |  ET |
|:---:|:---:|:---:|\n'''

for a in [True,False]:
    for b in [True,False]:
        table += f"|  {a}  |  {b}  |  {a and b}  |\n"
        
Markdown(table)        

Fontion OU (OR) :¶

La disjonction dont l'expression booléenne est a or b, est réalisée lorsqu'au moins l'une des conditions a ou b est réalisée :

a	b	OU
0	0	0
0	1	1
1	0	1
1	1	1

Equation booléenne : $a + b = a | b = a ∨ b$

A programmer vous-même :

In [ ]:

# Table de vérité en Markdown par  Python de l'opérateur OU :

Fontion NON (NOT) :¶

La négation dont l'expression booléenne est not a, est réalisée lorsque la condition a n'est pas réalisée :

A	NON
0	1
1	0

Equation booléenne : $\bar{a} =$ ~$a = ¬a$

A programmer vous-même :

In [ ]:

# Table de vérité en Markdown par Python de l'opérateur NON :

Autres Fonctions logiques :¶

A partir des trois fonctions de bases ET, OU, NON, on peut en construire d'autres telles que :

Fonction OU-Exclusif (XOR) :¶

A	B	NOR
0	0	0
0	1	1
1	0	1
1	1	0

A programmer vous-même :

Vérifier que les expressions booléennes ((not a) and b) or (a and (not b)) et a ^ b sont équivalentes.

In [ ]:

# Table de vérité en Markdown par Python de l'opérateur OU-Exclusif :

Fonction NON-ET (NAND) :¶

A	B	NAND
0	0	1
0	1	1
1	0	1
1	1	0

A programmer vous-même :

Vérifier que les expressions booléennes not (a and b) et (not a) or (not b) sont équivalentes.

In [ ]:

# Table de vérité en Markdown par Python de l'opérateur NON-ET :

Fonction NON-OU (NOR) :¶

A	B	NOR
0	0	1
0	1	0
1	0	0
1	1	0

A programmer vous-même :

Vérifier que les expressions booléennes not (a or b) et (not a) and (not b) sont équivalentes.

In [ ]:

# Table de vérité en Markdown par Python de l'opérateur NON-OU :

Les lois de De Morgan :
$$\overline{a \bullet b} = \overline{a} + \overline{b}$$$$\overline{a + b} = \overline{a} \bullet \overline{b}$$
Exemple : Le contraire d'être riche et célèbre est ................................

Application à l'addition binaire :¶

In [ ]:

from metakernel import register_ipython_magics
register_ipython_magics()

In [ ]:

%%tutor

n = [0, 1, 0]
p = [0, 1, 1]
r = []

c = False
for i in range(2, -1, -1):
    a = n[i]
    b = p[i]
    unite = (a and not(b) and not(c)) or\
        (not(a) and b and not(c)) or\
        (not(a) and not(b) and c) or\
        (a and b and c)
    r = [int(unite)] + r
    c = (a and b) or (b and c) or (a and c)
r = [int(c)] + r

print(r)

Opération booléenne bit à bit :¶

Dans beaucoup de langages, and et or sont écrits && et ||.

Ces symboles existent égalemant en Python, mais ils sont là pour réaliser des opérations binaires bit à bit :

In [ ]:

masque = 0b00001111
resultat = 0b10011101 & masque
resultat, bin(resultat), hex(resultat)

Les 1 du masque définissent les bits qui seront conservés dans le résultat.

In [ ]:

bin(0b10011101 | 0b00001111)

In [ ]:

bin(0b10011101 ^ 0b00001111)

A faire vous-même :

Calculer les opérations binaires suivantes :

# calcul A
   1100
&  0111
----------


# calcul B
   1100
|  0111
----------


# calcul C
   1100
^  0111
----------


# calcul D
~  1100
&  0111
----------

Vérifier vos résultats avec Python en décimal, puis en binaire et en hexadécimal :

In [ ]:

# calcul A
12 & 7

In [ ]:

# calcul B
12 | 7

In [ ]:

# calcul C
12 ^ 7

In [ ]:

# calcul D
~12 & 7

Le OU exclusif (XOR) est une méthode de cryptographie moderne qui s'est développée avec l'avènement de l'informatique. Elle consiste à chiffrer un message en binaire avec une clé répétée par une multiplication par OU Exclusif.

Ainsi le chiffrement de la chaine de caractères 'NSI' avec la clé 'f' produit '(5/'...

Caractère séquentiel (shortcuts) :¶

En Python, les opérateurs and et or sont séquentiels : L'opérande de droite n'est évaluée que si l'opérande de gauche ne permet pas de trouver le résultat. On parle d'évaluation fainéante...

Pour a and b :

Si a est False, inutile d'évaluer b, ce sera False ;
Si a est True, alors il faudra évaluer b pour savoir.

Pour a or b :

si a est True, inutile d'évaluer b, ce sera True ;
si a est False, il faudra évaluer b pour savoir.

Illustration : http://sametmax.com/quelques-astuces-a-propos-de-and-et-or/

Applications :¶

Google doodle

Répondre aux questions du notebook Capytale n° 0e33-4601596

Portes logiques

Observer la représentation des portes logiques (NON, ET, OU, NON-ET, NON-OU, OU-EXCLUSIF) et réaliser des schémas de circuits pour simuler leur fonctionnement sur Capytale n° 513c-4629553 (ou sur https://logic.ly/demo)

BBC micro:bit

Programmer puis expérimenter le fonctionnement de chaque fonction logique (NON, ET, OU, NON-ET, NON-OU, OU-EXCLUSIF) avec une carte BBC micro:bit

utiliser les boutons-poussoir A et B pour faire les entrées et afficher en sortie sur la matrice à LEDs un pour vrai et un pour faux ;
conserver une copie de vos programme MicroPython dans un notebook sur Capytale n° 96d9-4637151 .

France IOI - Zones de couleurs :

Ce que doit faire votre programme :

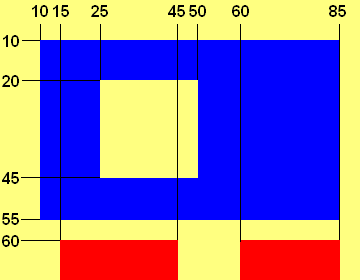
Sur une table est placée une feuille de papier rectangulaire de 90 cm de large et 70 cm de haut, composée de zones de différentes couleurs, comme le décrit la figure ci-dessous. Un certain nombre de personnes placent l'une après l'autre un jeton où elles le souhaitent sur la table, à l'exception des frontières entre les différentes zones.

On vous donne en entrée le nombre de jetons qui ont été déposés, puis, pour chaque jeton, ses coordonnées sur la feuille par rapport à l'origine en haut à gauche, sous la forme d'une abscisse et d'une ordonnée entre −1 000 et 1 000.

Votre programme devra qualifier chaque jeton avec l'un des textes suivants, en fonction de la couleur sur laquelle il se trouve :

« En dehors de la feuille »
« Dans une zone jaune »
« Dans une zone bleue »
« Dans une zone rouge »

Essayez d'écrire votre programme de sorte qu'il y ait au maximum une condition par possibilité de texte affiché.

Exemple

entrée :

sortie :

Dans une zone bleue
Dans une zone jaune
Dans une zone rouge
En dehors de la feuille

Commentaires

Dans l'exemple, on a 4 jetons, de coordonnées (16 ; 12), (30 ; 22), (64 ; 62) et (-5 ; 86).

Tester votre programme sur France IOI...

In [ ]:

# Votre code

In [ ]:

# Votre code d'animation avec ipycanvas

Références aux programmes :¶

Contenus	Capacités attendues	Commentaires
Valeurs booléennes : 0,1. Opérateurs booléens : and, or, not. Expressions booléennes.	Dresser la table d’une expression booléenne.	Le ou exclusif (xor) est évoqué. Quelques applications directes comme l’addition binaire sont présentées. L’attention des élèves est attirée sur le caractère séquentiel de certains opérateurs booléens.

Pour Aller plus loin :¶

Ce document est mis à disposition selon les termes de la Licence Creative Commons Attribution - Partage dans les Mêmes Conditions 4.0 International.

Pour toute question, suggestion ou commentaire : eric.madec@ecmorlaix.fr

In [ ]: