Notebook

Programmation dynamique¶

Illustration avec la suite de Fibonacci définie par :

$F_0 = 0$
$F_1 = 1$
$\forall n \in \mathbb{N}, F_{n+2} = F_{n+1}+F_n$

Approche récursive¶

Simple

In [ ]:

def fibo(n):
    if n == 0 :
        return 0   
    elif n == 1 :
        return 1
    else :
        return fibo(n-1) + fibo(n-2)

In [ ]:

fibo(3)

In [ ]:

from metakernel import register_ipython_magics
register_ipython_magics()

In [ ]:

%%tutor

def fibo(n):
    if n == 0 :
        return 0   
    elif n == 1 :
        return 1
    else :
        return fibo(n-1) + fibo(n-2)

fibo(3)

Mais inefficace

Le temps de calcul est de plusieurs dizaines de secondes, sur une machine récente.

In [ ]:

import time

def fibo(n):
    if n == 0 :
        return 0   
    elif n == 1 :
        return 1
    else :
        return fibo(n-1) + fibo(n-2)
            
t0 = time.time()
fibo(40)
print(time.time() - t0)

En cause : la multitude des appels récursifs nous conduit à refaire des calculs déjà effectués.

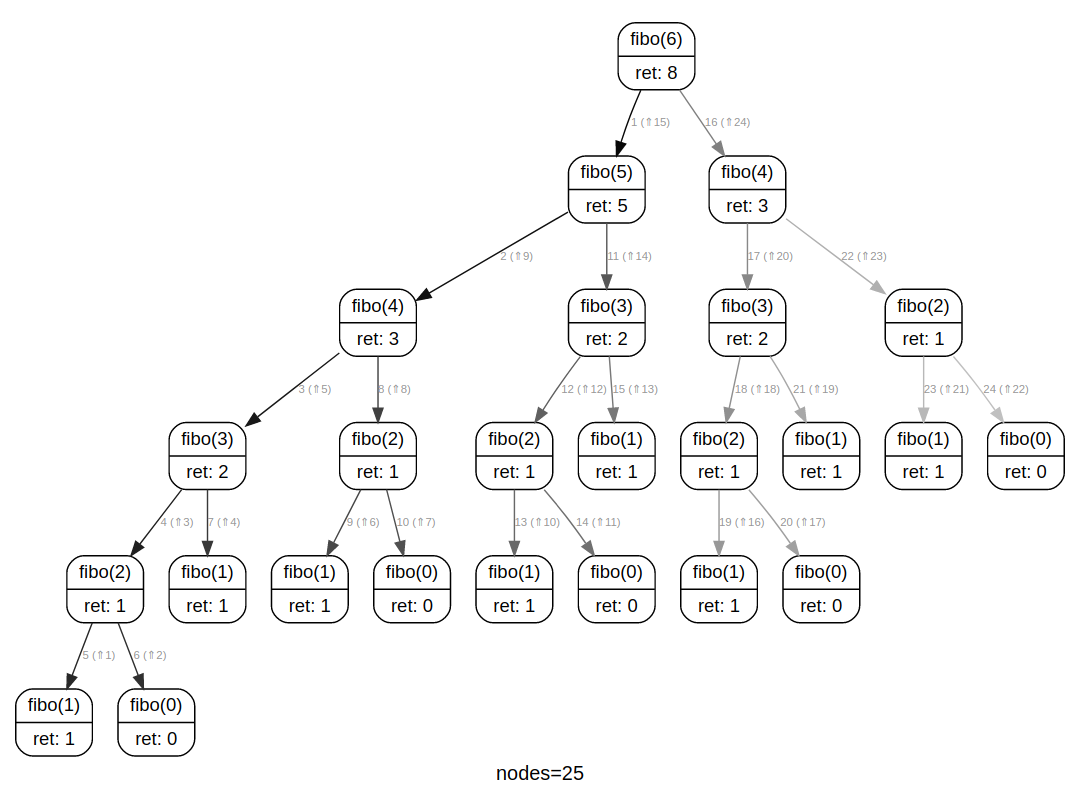
Le calcul de fibo(2) se retrouve ainsi 5 fois dans l'arbre.

Pour résoudre notre problème, on le divise en problèmes plus petits, mais contrairement aux algorithmes de dichotomie, ou du tri-fusion, ici les problèmes ne sont pas indépendants. Une approche par diviser pour régner est donc impossible.

Les problèmes se recouvrent, ce qui nous amène à refaire des choses déjà faites.

La mémoïsation¶

Pour éviter de recalculer (par exemple) 5 fois fibo(2) on peut stocker le résultat de chaque calcul, par exemple dans un dictionnaire. Ainsi, à chaque demande de calcul :

Soit le calcul a déjà été effectué : on a donc juste à le lire dans le dictionnaire.
Soit le calcul n'a jamais été effectué : on l'effectue, et on stocke le résultat dans le dictionnaire.

In [ ]:

%%tutor

dict_fibo = {0:0, 1:1}
def fibo(n):
    if n in dict_fibo:
        return dict_fibo[n]
    dict_fibo[n] = fibo(n-1) + fibo(n-2)
    return dict_fibo[n]

fibo(3)

In [ ]:

import time
          
t0 = time.time()
fibo(40)
print(time.time() - t0)

In [ ]:

dict_fibo

Remarques¶

Le dictionnaire (global) dict_fibo doit être à l'extérieur de la fonction, sinon il est réinitialisé à chaque appel récursif !

Un dictionnaire (global) étant un type mutable, sa modification à l'intérieur de la fonction ne pose pas de problème. Toutefois, ce genre de pratique est déconseillé : si par exemple on appelle 2 fois la fonction fibo, le dictionnaire n'est pas réinitialisé entre-temps (ce qui dans notre cas n'est pas problématique, mais cela pourrait l'être).

Pour éviter cela on peut utiliser une fonction englobante (appelée ici fibonacci ) :

In [ ]:

def fibonacci(n):
    dict_fibo = {0:0, 1:1}
    def fibo(n):
        if n in dict_fibo:
            return dict_fibo[n]
        dict_fibo[n] = fibo(n-1) + fibo(n-2)
        return dict_fibo[n]
    return fibo(n)

In [ ]:

fibonacci(50)

Observez la définition d'une fonction à l'intérieur d'une autre. Cela ne pose aucun problème, mais attention, cette fonction n'existe pas à l'extérieur de sa fonction englobante.

Mémoïsation automatique en Python¶

La fonction lru_cache du module functools permet de mémoïser automatiquement une fonction récursive. Il suffit, juste avant d'écrire la fonction, de mettre la ligne @lru_cache (appelée décorateur).

In [ ]:

import time
from functools import lru_cache

@lru_cache  #(1)
def fibo(n): #(2)
    if n == 0 :
        return 0   
    elif n == 1 :
        return 1
    else :
        return fibo(n-1) + fibo(n-2)
    
t0 = time.time()
fibo(35)
print(time.time() - t0)

Méthode top-down vs bottom-up¶

La structure récursive naturelle de la suite de Fibonacci nous a conduit vers un programme qui calcule (ou plutôt appelle) les valeurs de haut en bas.

Et si on commençait par le bas ?

Si nous devions calculer mentalement le 6ème terme de la suite de Fibonacci, on commencerait par calculer le 3ème, puis le 4ème, puis le 5ème et enfin le 6ème.

In [ ]:

def fibo(n):
    dict_fibo = {}
    dict_fibo[0] = 0
    dict_fibo[1] = 1
    for k in range(2, n+1):
        dict_fibo[k] = dict_fibo[k-1] + dict_fibo[k-2]
    return dict_fibo[n]

Cette méthode itérative part du bas pour aller vers le haut. On parle de méthode bottom-up. De manière plus générale, cette méthode est basée sur le fait de résoudre des problèmes de petite taille, puis de plus en plus gros, jusqu'au problème final.

Bilan des méthodes¶

Lors d'un calcul effectué de manière récursive, il peut arriver que de multiples appels récursifs soient identiques. Pour éviter de recalculer plusieurs fois la même chose, on peut stocker les résultats intermédiaires. On appelle cette technique la mémoïsation.

Cette technique minimise le nombre d'opérations et accélère grandement l'exécution du programme. Le prix à payer est l'utilisation d'une structure de stockage des valeurs intermédiaires, et donc une augmentation de la mémoire utilisée par le programme.

Lors d'un calcul effectué de manière itérative, il est parfois plus simple de commencer par une «petite» version du problème pour progressivement remonter vers la solution du problème global.