Structure linéaire de données : Pile¶
En informatique on manipule essentiellement des données.
Une structure de données est une organisation logique des données permettant de simplifier ou d'accélérer leur traitement.
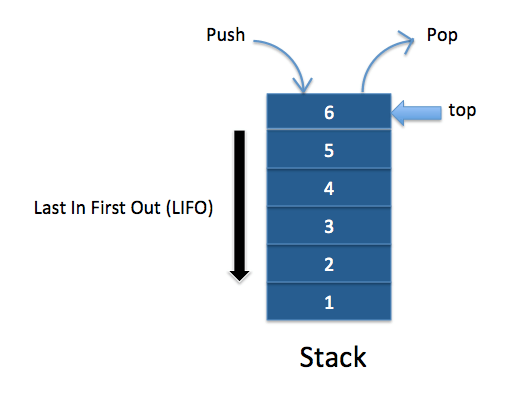
Une pile (stack en anglais) est une structure de données fondée sur le principe du «dernier arrivé, premier sorti» (ou LIFO pour Last In, First Out), ce qui veut dire que les derniers éléments ajoutés à la pile seront les premiers à être récupérés.
Le fonctionnement est donc celui d’une pile d’assiettes : on ajoute (push) des assiettes sur la pile, et on les récupère (pop) dans l’ordre inverse, en commençant par la dernière ajoutée.
Voici quelques exemples d’usage courant d’une pile :
- Dans un navigateur web, une pile sert à mémoriser les pages Web visitées. L’adresse de chaque nouvelle page visitée est empilée et l’utilisateur dépile l’adresse de la page précédente en cliquant le bouton «Afficher la page précédente».
- La fonction «Annuler la frappe» (en anglais «Undo»)(touches
CTRL+Z) d’un traitement de texte mémorise les modifications apportées au texte dans une pile. - L’évaluation des expressions mathématiques en notation post-fixée (ou polonaise inverse), qui a été implantée dans certaines calculatrices Hewlett-Packard, utilise une pile...
TAD d'une pile :¶
On retrouve dans les piles une partie des propriétés vues sur les listes. Dans les piles, il est uniquement possible de manipuler le dernier élément introduit dans la pile.
Pour définir une structure de pile, outre son initialisation, on a besoin d’un nombre réduit d’opérations de bases :
- «empiler» : ajoute un élément sur la pile. En anglais : « push » ;
- «dépiler» : enlève un élément de la pile et le renvoie. En anglais : « pop » ;
- «vide» : renvoie vrai si la pile est vide, faux sinon ;
- «remplissage» : renvoie le nombre d’éléments dans la pile.
La structure de pile est un concept abstrait, pour la réaliser dans la pratique, plusieurs implémentations sont possibles...
Implémentation :¶
Version 1 :¶
En utilisant une liste "built in" de Python pour représenter la pile.
Il se trouve que les méthodes append et pop sur les listes jouent déjà le rôle de push et pop sur les piles.
Voici les fonctions de base :
def pile():
#retourne une liste vide
return []
# vide
def vide(p):
'''renvoie True si la pile est vide et False sinon'''
return p==[]
# empiler
def empiler(p,x):
'''Ajoute l’élément x à la pile p'''
p.append(x)
# dépiler
def depiler(p):
'''dépile et renvoie l’élément au sommet de la pile p'''
assert not vide(p), "Pile vide"
return p.pop()
A faire vous même n°1 :
Tester les instructions suivantes :
p = pile()
for i in range(5):
empiler(p,2*i)
a = depiler(p)
print(a)
print(vide(p))
A faire vous même n°2 :
Réaliser les fonctions taille(p) et sommet(p) qui retournent respectivement la taille de la liste et le sommet de la liste (sans le supprimer).
def taille(p) :
def sommet(p) :
Version 2 :¶
En définissant une classe Pile pour implémenter cette structure :
class Pile :
'''classe Pile création d’une instance Pile avec une liste'''
def __init__(self):
'''Initialisation d’une pile vide'''
self.L=[]
def vide(self):
'''teste si la pile est vide'''
return self.L==[]
def depiler(self):
'''dépile'''
assert not self.vide(),"Pile vide"
return self.L.pop()
def empiler(self,x):
'''empile'''
self.L.append(x)
A faire vous même n°3 :
Tester les instructions suivantes :
p = Pile()
for i in range(5) :
p.empiler(2*i)
print(p.L)
a = p.depiler()
print(a)
print(p.L)
print(p.vide())
A faire vous même n°4 :
Réaliser les méthodes taille(self) et sommet(self) qui retournent respectivement la taille de la liste et le sommet de la liste (sans le supprimer).
Exercice d'application 1 : Contrôle du parenthésage d’une expression
Il s’agit d’écrire une fonction qui contrôle si une expression mathématique, donnée sous forme d’une chaîne de caractères, est bien parenthésée, c’est- à-dire s’il y a autant de parenthèses ouvrantes que de fermantes, et qu’elles sont bien placées.
Par exemple :
- (..(..)..) est bien parenthésée
- (...(..(..)...) ne l’est pas:
L’algorithme :¶
On crée une pile.
On parcourt l’expression de gauche à droite.
À chaque fois que l’on rencontre une parenthèse ouvrante "( " on l’empile.
Si on rencontre une parenthèse fermante " ) " et que la pile n’est pas vide on dépile (sinon on retourne faux)
À la fin la pile doit être vide...
A faire vous même n°5 :
Écrire en pseudo code l’algorithme
...
...
A faire vous même n°6 :
En utilisant l’une des structures pile réalisées plus haut, écrire une fonction verification(expr) qui vérifie si une expression mathématique passée en paramètre est correctement parenthésée :
A faire vous même n°7 :
Faire en sorte que le programme tienne compte également des [...
Exercice d'application 2 : Convertisseur décimal => binaire
Petit rappel :¶
Une méthode de conversion consiste à diviser le nombre décimal à convertir par la base b et conserver le reste de la division. Le quotient obtenu est divisé par b et conserver le reste. Il faut répéter l’opération sur chaque quotient obtenu.
Par exemple, pour la conversion : $91$ = $01011011_2$

Les restes successifs sont écrits, en commençant par le dernier, de la gauche vers la droite. Cette méthode est dite « Méthode des divisions successives ».
A faire vous même n°7 :
Écrire une fonction decToBin(n) qui prend en paramètre un entier n et qui renvoie l’écriture binaire de cet entier en utilisant une pile pour stocker les restes des divisions successives.
A faire vous même n°8 :
Écrire une fonction baseConverter(n,b) qui prend en paramètres 2 entiers (avec 2 ≤ b ≤ 16) et qui renvoie l’écriture en base b de cet entier en utilisant une pile pour stocker les restes des divisions successives.
Références aux programmes :¶
Structures de données
| Contenus | Capacités attendues | Commentaires |
|---|---|---|
| Listes, piles, files : structures linéaires. Dictionnaires, index et clé. |
Distinguer des structures par le jeu des méthodes qui les caractérisent. Choisir une structure de données adaptée à la situation à modéliser. Distinguer la recherche d’une valeur dans une liste et dans un dictionnaire. |
On distingue les modes FIFO (first in first out) et LIFO (last in first out) des piles et des files. |

Ce document, basé sur le travail de Stephan VAN ZUIJLEN, est mis à disposition selon les termes de la Licence Creative Commons Attribution - Partage dans les Mêmes Conditions 4.0 International.
Pour toute question, suggestion ou commentaire : eric.madec@ecmorlaix.fr