Deep Learning in Python¶
Session 01 - Introduction to Keras¶
- Course: Big Data and Language Technologies
- Date: 04.04.2022
In this session, we'll start with one of the most basic tasks in Natural Language Processing: training a model on text data to assign a numerical value between 0 and 1 corresponding to a single target feature. In this first session, we are going to use the IMDB Movie Review Dataset to perform sentiment classification, where 0 is negative sentiment, and 1 is positive sentiment.
Errata¶
- 2022/04/11: changed the tokenization to be fitted on training samples only
Preface¶
This notebook...
... may feel basic if you've done statistical modeling or machine learning before. Don't worry, we will progress to more in-depth topics – these first sessions are thought to get everyone, regardless of their background and prior experience on the same level.
... is divided into three steps:
- Load and preprocess the IMDB dataset
- Build a basic TensorFlow model using the Keras API
- Evaluate and select the best model and perform inference on unseen data
... assumes three things:
- You have successfully completed the
101-Setup.mdguide and thus have a working environment with all dependencies installed - You understand the basics of neural machine learning, with concepts like neurons, activation functions, loss functions, and optimization strategies
- You work in a UNIX-based environment (Linux, MacOS); if you're on Windows, you might need to adapt shell commands to your specific case
... is organized as follows: each block of code cells is prefaced with a text cell containing a general explanation, then an Exercise (describing what is to be achieved in the following code cells), and optionally Notes (providing hints for the solution). Code cells might already contain some comments to help you along the way.
Setup¶
# Core packages
import pandas as pd # High-level data wrangling
import numpy as np # Low-level data wrangling
import tensorflow as tf # All the neural stuff
# Helper functions
from sklearn.model_selection import train_test_split # Splits a dataset randomly into train and test subsets
from glob import glob # Expands a wildcard paths to all matching files for traversal
Importing Data¶
The data can be downloaded by running the following cell. This will retrieve the archive and decompress it in your current directory.
#!curl -O https://ai.stanford.edu/~amaas/data/sentiment/aclImdb_v1.tar.gz
#!tar -xf aclImdb_v1.tar.gz
We now need to convert the dataset into a form that we can explore and train models on.
Exercise: load all the data into a pandas.DataFrame with the four columns [id, text, label, set] and one document per row.
idis the documents' IDtextis the documents' textlabelis the documents labelled sentiment:negorpossetis the document set the document stems from:trainortest
df = []
PATH = "./aclImdb/"
SETS = ["train", "test"]
LABELS = ["neg", "pos"]
for doc_set in SETS:
for label in LABELS:
for file in glob(PATH+doc_set+"/"+label+"/*.txt"):
file_id = file.split("/")[-1].split(".")[0]
with open(file, "r") as f:
text = f.read()
doc = (file_id, text, label, doc_set)
df.append(doc)
df = pd.DataFrame(df, columns=["id", "text", "label", "set"])
df.head()
| id | text | label | set | |
|---|---|---|---|---|
| 0 | 1821_4 | Working with one of the best Shakespeare sourc... | neg | train |
| 1 | 10402_1 | Well...tremors I, the original started off in ... | neg | train |
| 2 | 1062_4 | Ouch! This one was a bit painful to sit throug... | neg | train |
| 3 | 9056_1 | I've seen some crappy movies in my life, but t... | neg | train |
| 4 | 5392_3 | "Carriers" follows the exploits of two guys an... | neg | train |
Preprocessing the Data¶
The next step is to preprocess the movie reviews. While for humans, the text and label as seen in the last step are interpretable, we cannot train a model directly on the text data: we need to convert texts and labels it into a numerical input and output space first.
Since train and test set are independently used, we perform this individually for both document sets.
Exercise: transform the text and label data into a suitable numeric representation. Encode the pos label as 1, and the neg label as 0. Convert all documents into sequences of term indices. The output should be the sequence sets X_train and X_test, and the label arrays y_train and y_test.
Notes
- Use the
tf.keras.preprocessing.text.Tokenizerclass to construct the document-term-matrix - Think about space savings in data types! An
int8ist 8 times smaller than the defaultint64data type. And since our data does not exceed the number space representable byint8, we can fit the same data into less memory.
# Create and fit the tokenizer on training set texts
tokenizer = tf.keras.preprocessing.text.Tokenizer()
tokenizer.fit_on_texts(df.loc[df["set"] == "train", "text"])
# Transform the training set documents into sequences
X_train = tokenizer.texts_to_sequences(df.loc[df["set"] == "train", "text"])
# Transform the test set documents into sequences
X_test = tokenizer.texts_to_sequences(df.loc[df["set"] == "test", "text"])
# Transform the training set labels into a 0-1 array
y_train = df.loc[df["set"] == "train", "label"].replace({"neg": 0, "pos": 1}).astype(np.int8).values
# Transform the test set labels into a 0-1 array
y_test = df.loc[df["set"] == "test", "label"].replace({"neg": 0, "pos": 1}).astype(np.int8).values
One problem remains: the model expects are input to be of equal length, yet the documents are varying. Therefore, they need to be padded with zeroes.
Exercise: pad all sequences with zero to uniform length of 256.
Notes
- use the
keras.preprocessing.sequence.pad_sequencesfunction - insert padding at the end of the sequences (post-padding)
X_train = tf.keras.preprocessing.sequence.pad_sequences(X_train, padding='post', maxlen=256)
X_test = tf.keras.preprocessing.sequence.pad_sequences(X_test, padding='post', maxlen=256)
While we now have individual document sets to train and test on, we want to further split the training set into an actual training set and the validation set that is used to check the models performance after each training iteration.
Exercise split the training data into an X_train/y_train and X_val/Y_val set with an 80/20 split.
X_train, X_val, y_train, y_val = train_test_split(X_train, y_train, test_size=0.2)
Building a Simple Neural Network¶
Sequential Network¶
A Sequential model is a plain stack of layers, where each layer has exactly one input tensor and one output tensor. If we add multiple layers to the model, the output of the first will be passed as input to the second, the output of the second will be passed as input to the third, and so on. Note that input each layer has to have the same dimensionality as the previous output.
The first and last layer are special: the first has to have an input dimensionality corresponding to the training data. The last layer has to have the dimensionality of the desired output.
Exercise: instatiate a keras.Sequential model.
model = tf.keras.Sequential()
Embedding Layer¶
A Sequential model behaves much like a list of layers: we can append to it using the keras.Sequential.add function, which takes the to-be-added layer as argument. First, we are going to add an input Embedding layer to the model.
An Embedding layer turns positive integers (the term index in our document sequences) into dense vectors of fixed size. For example, we can turn a sequence of two indices into a two-dimensional vector of size two each:
So, why do we need it? There are two reasons our Sequential model begins with an Embedding layer.
The first is that we want to build a semantic representation of words, i.e. a vector space in which the distance between words relates to their semantic closeness. This is what the Embedding layer does: it transforms the discrete (word index) input space into a dense continuous vector space.
The second reason is efficiency. The model cannot operate term indices directly, but instead needs a vectorized input. One option would be to use one-hot encoding to represent each index as a vector. For example, the index 44 in a vocabulary of 500 terms would be turned into a vector of 500 zeroes where the 44th place is a one. This leaves us with a vector representation that is both of extremely high dimensionality and extremely sparse - both are inefficient. The Embedding layer increases the efficiency by using much smaller, dense vectors. The index 44 can now be represented as a 16-dimension vector with continous, dense values.
Taking both together, the Embedding layer increases both the efficiency and effectiveness of our network.
Exercise: add an keras.layers.Embedding layer with 16 latent dimensions to the model.
Notes
- you can get the vocabulary size (i.e. input dimensionality) from the tokenizer.
- remember to add 1 to the vocabulary size, since we have padded our sequence data with zeroes, which created an additional "empty" term.
vocab_size = len(tokenizer.word_index)+1
model.add(tf.keras.layers.Embedding(vocab_size, 16))
Pooling Layer¶
The previous Embedding layer produces an output tensor of size (batch_size, 256, 16) - the 256 is the sequence length we padded our documents to, and we have 16 latent dimensions in our term embeddings. Do not worry about the batch_size for now, it will be explained later.
We cannot feed this tensor directly into a Dense layer: we still have a 3D tensor, but a Dense layer only accepts a 2D tensore as input. Enter: the Pooling layer. It performs a pooling operation to collapse one dimension of the tensor. In our case, we are going to use a GlobalAveragePooling1D layer: it calculates the average over one dimension of the input, collapsing it to a single number. You can think about this are reducing all the individual term embeddings into a single aggregated sequence embedding. The output dimensionality is therefore (batch_size, 16).
Exercise: add a keras.layers.GlobalAveragePooling1D layer to the model.
model.add(tf.keras.layers.GlobalAveragePooling1D())
Dense Layer¶
The next layer is a Dense layer: just your regular densely-connected neural layer, where $n$ inputs (in our case 16) are fully connected to $m$ output neurons (in our case 16, too). The Dense layer needs an activation function (ref. Lecture). We are going to use a fairy simple one: a ReLU (Rectifying Linear Unit).

It is just a linear activation of the input, that cannot fall below 0.
Exercise: add a keras.layers.Dense layer with 16 dimensions and a ReLU activation function to the model.
Notes:
- the ReLU function is implemented as
tf.nn.relu
model.add(tf.keras.layers.Dense(16, activation=tf.nn.relu))
Dropout Layer¶
To increase the robustness of our model, the layer is a Dropout layer. The Dropout layer randomly sets input units to 0 at each step during training time. This is also referred to as regularization (similar to regularization in linear regression problems) and helps prevent overfitting.
Exercise: add a keras.layers.Dropout layer with a dropout rate of 0.1 to the model.
model.add(tf.keras.layers.Dropout(0.1))
Output Layer¶
The last layer of the model reduces the dimension of the output to the desired size. From the previous Dropout layer, we still have 16-dimensional tensors, but we want to have a single value between 0 and 1 to express the sentiment of the input.
This is achieved by adding another Dense layer, but this time with an output dimensionality of 1. Also, our activation function changes: we are going to use a Sigmoid activation.
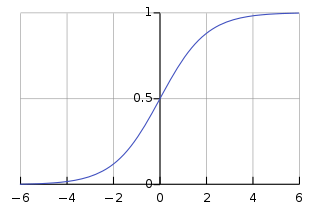
Exercise: add a keras.layers.Dense layer with 1 dimension and a sigmoid activation function to the model.
Notes:
- the sigmoid activation function is implemented as
tf.nn.sigmoid
model.add(tf.keras.layers.Dense(1, activation=tf.nn.sigmoid))
Model Summary¶
And thats it. We now have build the complete neural model to conduct sentiment classification. Before we continue, we will have a look at the model summary.
model.summary()
Model: "sequential"
_________________________________________________________________
Layer (type) Output Shape Param #
=================================================================
embedding (Embedding) (None, None, 16) 1417328
global_average_pooling1d (G (None, 16) 0
lobalAveragePooling1D)
dense (Dense) (None, 16) 272
dropout (Dropout) (None, 16) 0
dense_1 (Dense) (None, 1) 17
=================================================================
Total params: 1,417,617
Trainable params: 1,417,617
Non-trainable params: 0
_________________________________________________________________
Note the signal flow of tensors within out model: the 3D output of the Embedding layer is reduced to 2D by the Pooling layer. This is kept by the following layers, and reduced to a single value in the last Dense layers. Also note the parameter counts for each layer: since Pooling and Dropout are just static operations on the tensors where nothing is learned, they dont have trainable parameters.
Compiling the model, Optimizer and Loss function¶
In order to train the model, we first have to compile it. To understand the concepts introduced in this step, recall the well-known mountain-descent metaphor for model training: you're on top of a mountain and try to get down (find the local minimum). But since there is heavy fog, you can only see your immediate surroundings. The gradient descent strategy would be to see where in your visible surroundings the descent down the mountain is steepest and move there.

Compilation is the final step in defining a model. It specifies three things that influence the training procedure:
A Loss function: the loss function is used to quantify the errors made during the learning process. Simply put, the lower the output value of the loss function, the better performing the model is; the training process therefore aims to minimize the loss. In the mountain-descent example, the loss indicates your current elevation.
An Optimizer: the optimizer strategy is used to calculate the direction and magnitude of parameter updates during gradient descent. In the mountain-descent example, the optimizer is how you detect where to move next.
A validation Metric: a metric is used to quantify the quality of the models predictions. While the loss quantifies the goodness-of-fit of the model parameters, the metric is calculated only on the output predictions of the model.
Exercise: compile the model using the adam optimizer, the binary_crossentropy loss function, and the accuracy metric.
model.compile(optimizer='adam',
loss='binary_crossentropy',
metrics=['acc'])
Callbacks¶
A callback is an action that is performed at a specific stage of training (e.g. at the start or end of an epoch, before or after a single batch, ...).
We are going to use callbacks to:
- save a checkpoint after each epoch if the validation loss improved
- abort training if no validation loss improvement is apparent for 10 epochs
Exercise: instantiate a keras.callbacks.ModelCheckpoint that saves the best model according to the validation loss.
Notes:
- Keras saved models are usually named with a
*.h5suffix
checkpoint = tf.keras.callbacks.ModelCheckpoint(
"imdbsent.h5", # Path to save the model file
monitor="val_loss", # The metric name to monitor
save_best_only=True # If True, it only saves the "best" model according to the quantity monitored
)
Exercise: instantiate a keras.callbacks.EarlyStopping that aborts training when no improvement in validation loss has taken place for 10 iterations.
Notes:
- Use a delta of $\pm 0.01$ to indicate improvement
early_stopping = tf.keras.callbacks.EarlyStopping(
monitor="val_loss", # Quantity to be monitored.
min_delta=0.01, # Minimum change in the monitored quantity to qualify as an improvement, i.e. an absolute change of less than min_delta, will count as no improvement.
patience=10, # Number of epochs with no improvement after which training will be stopped.
)
Training the Model¶
At this point, we assembled all components needed to train our first model:
- preprocessed training, testing, and validation datas
- model architecture
- callbacks
Exercise: fit the model on the training data for 100 epochs with a batch size of 512, evaluation on the validation subset. Use both previously instantiated callback functions.
history = model.fit(
X_train,y_train,
epochs=100,
validation_data=(X_val, y_val),
verbose=1, # print result every epoch
batch_size=512,
callbacks = [checkpoint, early_stopping]
)
Epoch 1/100 1/40 [..............................] - ETA: 6s - loss: 0.6931 - acc: 0.4883
2022-04-11 13:54:33.552966: W tensorflow/core/platform/profile_utils/cpu_utils.cc:128] Failed to get CPU frequency: 0 Hz
40/40 [==============================] - 1s 11ms/step - loss: 0.6913 - acc: 0.6041 - val_loss: 0.6876 - val_acc: 0.7304 Epoch 2/100 40/40 [==============================] - 0s 9ms/step - loss: 0.6809 - acc: 0.7286 - val_loss: 0.6718 - val_acc: 0.7934 Epoch 3/100 40/40 [==============================] - 0s 9ms/step - loss: 0.6568 - acc: 0.7830 - val_loss: 0.6399 - val_acc: 0.8008 Epoch 4/100 40/40 [==============================] - 0s 10ms/step - loss: 0.6138 - acc: 0.8002 - val_loss: 0.5912 - val_acc: 0.8172 Epoch 5/100 40/40 [==============================] - 0s 10ms/step - loss: 0.5561 - acc: 0.8240 - val_loss: 0.5340 - val_acc: 0.8324 Epoch 6/100 40/40 [==============================] - 0s 10ms/step - loss: 0.4941 - acc: 0.8468 - val_loss: 0.4771 - val_acc: 0.8472 Epoch 7/100 40/40 [==============================] - 0s 11ms/step - loss: 0.4339 - acc: 0.8674 - val_loss: 0.4266 - val_acc: 0.8612 Epoch 8/100 40/40 [==============================] - 0s 11ms/step - loss: 0.3800 - acc: 0.8850 - val_loss: 0.3853 - val_acc: 0.8716 Epoch 9/100 40/40 [==============================] - 0s 11ms/step - loss: 0.3366 - acc: 0.8961 - val_loss: 0.3521 - val_acc: 0.8770 Epoch 10/100 40/40 [==============================] - 0s 11ms/step - loss: 0.2971 - acc: 0.9079 - val_loss: 0.3273 - val_acc: 0.8820 Epoch 11/100 40/40 [==============================] - 0s 12ms/step - loss: 0.2655 - acc: 0.9158 - val_loss: 0.3085 - val_acc: 0.8860 Epoch 12/100 40/40 [==============================] - 0s 12ms/step - loss: 0.2405 - acc: 0.9258 - val_loss: 0.2939 - val_acc: 0.8884 Epoch 13/100 40/40 [==============================] - 0s 12ms/step - loss: 0.2189 - acc: 0.9317 - val_loss: 0.2833 - val_acc: 0.8910 Epoch 14/100 40/40 [==============================] - 0s 12ms/step - loss: 0.1992 - acc: 0.9380 - val_loss: 0.2749 - val_acc: 0.8932 Epoch 15/100 40/40 [==============================] - 0s 12ms/step - loss: 0.1819 - acc: 0.9451 - val_loss: 0.2688 - val_acc: 0.8946 Epoch 16/100 40/40 [==============================] - 0s 12ms/step - loss: 0.1673 - acc: 0.9506 - val_loss: 0.2633 - val_acc: 0.8970 Epoch 17/100 40/40 [==============================] - 0s 12ms/step - loss: 0.1541 - acc: 0.9536 - val_loss: 0.2609 - val_acc: 0.8974 Epoch 18/100 40/40 [==============================] - 0s 12ms/step - loss: 0.1430 - acc: 0.9578 - val_loss: 0.2571 - val_acc: 0.8986 Epoch 19/100 40/40 [==============================] - 0s 12ms/step - loss: 0.1317 - acc: 0.9610 - val_loss: 0.2556 - val_acc: 0.8998 Epoch 20/100 40/40 [==============================] - 0s 12ms/step - loss: 0.1223 - acc: 0.9647 - val_loss: 0.2536 - val_acc: 0.9010 Epoch 21/100 40/40 [==============================] - 0s 12ms/step - loss: 0.1134 - acc: 0.9690 - val_loss: 0.2526 - val_acc: 0.9014 Epoch 22/100 40/40 [==============================] - 0s 12ms/step - loss: 0.1042 - acc: 0.9730 - val_loss: 0.2529 - val_acc: 0.9002 Epoch 23/100 40/40 [==============================] - 0s 12ms/step - loss: 0.0975 - acc: 0.9747 - val_loss: 0.2547 - val_acc: 0.8998 Epoch 24/100 40/40 [==============================] - 0s 11ms/step - loss: 0.0907 - acc: 0.9778 - val_loss: 0.2535 - val_acc: 0.9012 Epoch 25/100 40/40 [==============================] - 0s 12ms/step - loss: 0.0839 - acc: 0.9787 - val_loss: 0.2544 - val_acc: 0.9002 Epoch 26/100 40/40 [==============================] - 0s 11ms/step - loss: 0.0785 - acc: 0.9809 - val_loss: 0.2559 - val_acc: 0.8996 Epoch 27/100 40/40 [==============================] - 0s 11ms/step - loss: 0.0730 - acc: 0.9833 - val_loss: 0.2584 - val_acc: 0.9002 Epoch 28/100 40/40 [==============================] - 0s 11ms/step - loss: 0.0678 - acc: 0.9844 - val_loss: 0.2602 - val_acc: 0.8998
Loading a Model¶
During training, the ModelCheckpoint callback continously persisted the best performing model to disk. Since the last epoch was not necessarily the best one, before we proceed with evaluation and inference, we can now load the best checkpoint to get the optimal model version.
Exercise: overwrite the model variable with the best performing version by loading the latest checkpoint from disk.
model = tf.keras.models.load_model("imdbsent.h5")
Evaluation¶
To quantify the true performance of the model, we are going to infer scores for the test set and compare them to the true gold labels, using accuracy as a metric. Since the model has not seen this data before, this score is expected to be lower than the valudation accuracy, yet allows us to gain insight into how well the model generalizes beyond its training data.
Exercise use the model evaluation function to calculate the test loss and accuracy.
score = model.evaluate(X_test, y_test, verbose=0)
print('Test loss:', round(score[0], 2))
print('Test accuracy:', round(score[1], 2))
Test loss: 0.3 Test accuracy: 0.88
Prediction¶
Finally, with the model trained and evaluated to ensure it produces reliable(ish) results, the only missing piece is prediction: inferring a sentiment judgement for any arbitrary input of text.
Exercise: write a predict(queries: np.array) -> np.array function that performs sentiment inference for a given unknown string. It should output sentiment scores in the range of [-1...1] (negative to positive)
Notes:
- the input string has to undergo the exact same preprocessing pipeline as the data the model was trained on (tokenization, padding, ...)
- it is customary to construct inference functions to take a batch of potentially many inputs and returns a list of predicted labels, instead of just a single query
- the model naturally outputs scores on the [0...1] range – you need to rescale that to the desired [-1...1] range
def predict(queries: np.array) -> np.array:
sequences = tokenizer.texts_to_sequences(queries)
sequences = tf.keras.preprocessing.sequence.pad_sequences(sequences, padding='post', maxlen=256)
return (model.predict(sequences) * 2) -1
Exercise: perform predictions for some sample inputs and see how well your model works. Can you find a case of clear misassignment, i.e. the model predicting wrong?
predict(["This is a good test sentence.", "This is perfect test sentence.", "This a a bad test sentence."])
array([[ 0.06828535],
[ 0.26398706],
[-0.28701127]], dtype=float32)
predict(["This is not a bad example at all."])
array([[-0.3305167]], dtype=float32)