M4W Series¶

Table of Contents

Chicken Tracks¶

Pecking away in the fertile dirt.

"Chicken Tracks" would usually be "scratches" (not tracks) but I wanted CT, the initials of Category Theory.

BEAST modules¶

These five "particles" are the objects that morph into one another.

Five things have ten relationships.

"To morph" is to literally "change shape" in this rendering of the Category concept. Think of a movie: of the shape changing.

To "ride a rail" from station A to station T is to go A2T. T2A is to go the other way. Play it backwards. We have twenty ways to go from x to y (x2y), counting each way as two-way.

In Polyhedrons we associate these 10 two-way edges with corresponding volume deltas. If a volume remains unchanged, even with a shape shift, then the corresponding x2y is 1. Such is the case between B, A and T. S2E is getting smaller and is < 1, whereas E2S is > 1, about 1.08 or $2\sqrt{7 - 3\sqrt{5}}$ to be precise.

Then there's which window to look through: IVM or XYZ?

Or we might think in terms of two language games, and which one to apply.

Nothing stops us from switching back and forth. The two unit volumes (cube : tetrahedron) have an S3 ratio $\sqrt(9/8)$, i.e. the cube is bigger, but not by a lot. It takes fewer unit cubes of water to fill the same volume, so the XYZ measure is smaller. Going from XYZ to IVM makes for a bigger volume number, .

Tetravolumes will showcase an IVM-based treatment, using the Quadray Coordinate System.

Switching Tracks¶

We want to get to recursivity early, so we might start opening doors into Lambda Calc in its formal initial glory.

Geographical factoid: Lambda Calc is associated with the Institute for Advanced Study at Princeton. Alonzo Church et al.

Per the nomenclature around here, Lambda Calc goes on to embrace differentiating characteristics keeping it distinguisable from Delta Calc, which is roughly delta calculus and math theories making use of continuous manifolds. The lambda stuff is more digital (discontinuous).

$$ \Lambda\ vs.\ \Delta $$

My thanks to Ryan Buchanan for bringing the following opus (a PDF) to my attention:

In [1]:

from IPython.display import YouTubeVideo

I see mention of Kleene. We've encountered one of Kleene's inventions previously: regular expressions.

The scribbles below are not a regular expression. Rather it's an example of what's called a T-predicate.

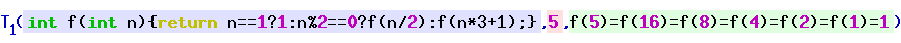
Example call of T1. The 1st argument gives the source code (in C rather than as a Gödel number e) of a computable function, viz. the Collatz function f. The 2nd argument gives the natural number i to which f is to be applied. The 3rd argument gives a sequence x of computation steps simulating the evaluation of f on i (as an equation chain rather than a Gödel sequence number). The predicate call evaluates to true since x is actually the correct computation sequence for the call f(5), and ends with an expression not involving f anymore. Function U, applied to the sequence x, will return its final expression, viz. 1.

Jochen Burghardt, CC BY-SA 4.0, via Wikimedia Commons

That Collatz function is interesting, what with that conjecture and all.

Lets do an equivalent implementation in Python:

In [2]:

def f(n : int) -> int:
    return 1 if n==1 else (f(n//2) if n%2==0 else f(n*3 + 1))

In [3]:

f(5)

Out[3]:

But we're not getting all the interim steps. Lets force a print:

In [4]:

def fp(n : int) -> int:
    """recursive collatz function"""
    print(f"f({n})")
    return 1 if n==1 else (
        fp(n//2) if n%2==0 
        else fp(n*3 + 1))

In [5]:

fp(5)

f(5)
f(16)
f(8)
f(4)
f(2)
f(1)

Out[5]:

In [6]:

fp(27)

f(27)
f(82)
f(41)
f(124)
f(62)
f(31)
f(94)
f(47)
f(142)
f(71)
f(214)
f(107)
f(322)
f(161)
f(484)
f(242)
f(121)
f(364)
f(182)
f(91)
f(274)
f(137)
f(412)
f(206)
f(103)
f(310)
f(155)
f(466)
f(233)
f(700)
f(350)
f(175)
f(526)
f(263)
f(790)
f(395)
f(1186)
f(593)
f(1780)
f(890)
f(445)
f(1336)
f(668)
f(334)
f(167)
f(502)
f(251)
f(754)
f(377)
f(1132)
f(566)
f(283)
f(850)
f(425)
f(1276)
f(638)
f(319)
f(958)
f(479)
f(1438)
f(719)
f(2158)
f(1079)
f(3238)
f(1619)
f(4858)
f(2429)
f(7288)
f(3644)
f(1822)
f(911)
f(2734)
f(1367)
f(4102)
f(2051)
f(6154)
f(3077)
f(9232)
f(4616)
f(2308)
f(1154)
f(577)
f(1732)
f(866)
f(433)
f(1300)
f(650)
f(325)
f(976)
f(488)
f(244)
f(122)
f(61)
f(184)
f(92)
f(46)
f(23)
f(70)
f(35)
f(106)
f(53)
f(160)
f(80)
f(40)
f(20)
f(10)
f(5)
f(16)
f(8)
f(4)
f(2)
f(1)

Out[6]:

In [7]:

YouTubeVideo("eTDH7m4vEiM")

Out[7]: