Packages¶

Install Packages¶

In [ ]:

using Pkg

In [ ]:

# CSV

Pkg.add(PackageSpec(url="https://github.com/JuliaData/CSV.jl#a1e02e68e2960dc35b25327174c2edca34c7f0fe"))

In [ ]:

# DataFrames

Pkg.add(PackageSpec(url="https://github.com/JuliaData/DataFrames.jl#fb4e184f3b3997da8680668fbf7fcc789811eb18"))

In [ ]:

# WebIO

Pkg.add(PackageSpec(url="https://github.com/JuliaGizmos/WebIO.jl#de95ec71ac81484f50ccd1db68d96f55380f8b6f"))

In [ ]:

#PlotlyJS

Pkg.add(PackageSpec(url="https://github.com/sglyon/PlotlyJS.jl#6580f9868ae8ada802eca8dc1327311b98436982"))

In [ ]:

# Interact

Pkg.add(PackageSpec(url="https://github.com/JuliaGizmos/Interact.jl#dd595cfd24feaaebba8c5456d5b7760f239b4241"))

In [ ]:

# Khepri

Pkg.add(PackageSpec(url="https://github.com/aptmcl/Khepri.jl#17885373412daf334663a8b68672542bc8e7861a"))

Using Packages¶

In [ ]:

using Logging

In [ ]:

Logging.disable_logging(Logging.Info)

In [ ]:

using CSV

In [ ]:

using DataFrames

In [ ]:

using WebIO

In [ ]:

using PlotlyJS

In [ ]:

using Interact

In [ ]:

using Base.Iterators

In [ ]:

using Khepri

In [ ]:

# Read the Julia file that contains the facade function
include("resources/optimization_facade.jl")

In [ ]:

# Read the Julia file that contains the optimzation functios
include("resources/optimization_main_functions.jl")

Macros¶

In [ ]:

avoid_tests = Parameter(true)

macro test(expr...)
  quote
    if !avoid_tests() 
        begin
            $(esc(expr...))
        end
    end
  end
end

In [ ]:

# avoid_tests(true)

In [ ]:

avoid_tests(false)

Weaved Façade¶

This design consists of a building envelope inspired by weaving techniques. Weaving is a traditional art technique wherein elements are interweaved following different strategies, creating 2D or 3D structures that benefit from both the material’s stiffness and color to create different textures/patterns.

inspiration 1	inspiration 2

Our weaving façade explores the application of this technique in architecture, namely, the tectonic and visual expressivities of weaving to generate a building skin with multiple geometric patterns and performance behaviors. Our façade design plays with the flexible nature of the weave-based patterns to manipulate shading, ventilation, and lighting proprieties inside the building.

Algorithmic Description¶

Main Functions¶

This section contains the main functions used to describe the weaved façade.

In [ ]:

transpose_matrix(matrix) =
    [[row[i] for row in matrix]
    for i in 1:length(matrix[1])]

In [ ]:

normals_surface(ptss)=
    [[quad_normal(p0,p1,p2,p3)
        for (p0,p1,p2,p3) in zip(pts[1:end-1],pts[2:end], next_pts[2:end], next_pts[1:end-1])]
    for (pts,next_pts) in zip(ptss[1:end-1],ptss[2:end])]

In [ ]:

normals_surface_extra_row(ptss)=
    let ptss1 = [vcat(pts,pts[end]) for pts in normals_surface(ptss)]
      [ptss1..., ptss1[end]]
  end

Description of parametric surfaces:

In [ ]:

struct Surf
    f::Function
    u0::Real
    u1::Real
    v0::Real
    v1::Real
end

In [ ]:

sub_surf(f::Function, u0::Real, u1::Real, v0::Real, v1::Real)=
    Surf(f, u0, u1, v0, v1)

In [ ]:

surf_pts(f::Function, u0::Real, u1::Real, v0::Real, v1::Real, n::Int, m::Int)=
    map_division(f, u0, u1, n, v0, v1, m)

Function that Creates the Axis of One Stripe¶

In [ ]:

backend(notebook)

In [ ]:

render_size(600, 400)

Façade composed of stripe-shaped elements
Undulating movement on the stripe's axis
Stripe’s original and undulating axes, represented by points

Spatial locations of the undulating shape.

In [ ]:

@test begin
ptss = map_division(xz, 0, 10, 10, 0, 10, 10)
nothing
end

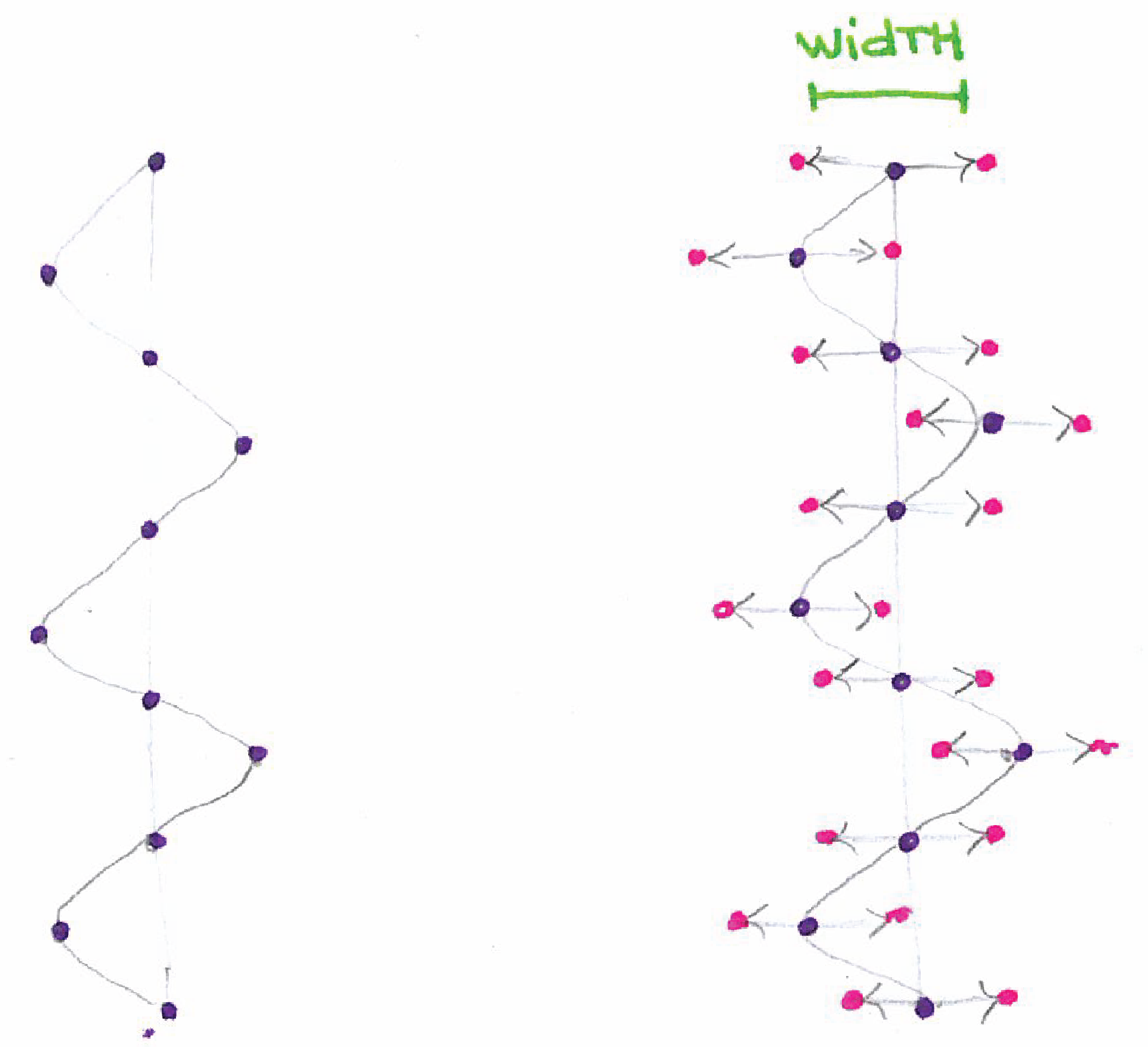
Version 1 (only amplitude)¶

Parameters: points and an amplitude value of the sinusoid

The algorithm moves the points in opposite perpendicular directions alternately, returning them as a new list of points

Sinusodial movement.

In [ ]:

stripe_2D_pts(pts, amp) =
    [let p1 = pt1 + vy(amp),
         p2 = pt2 - vy(amp)
      [p1, intermediate_loc(p1, p2, 0.5)]
     end
     for (pt1, pt2)
     in zip(pts, [pts[2:end]...,pts[end]])]

Test stripe_2D_pts function. The expected result is a 2D undulating spline:

In [ ]:

@test begin
new_backend()

pts = ptss[1]

@manipulate for amp=widget(0:0.01:1, label="Spline Amplitude")
                delete_all_shapes()
                spline(vcat(stripe_2D_pts(pts, amp)...)[1:end-1])
                nothing
            end
end

Expected result:

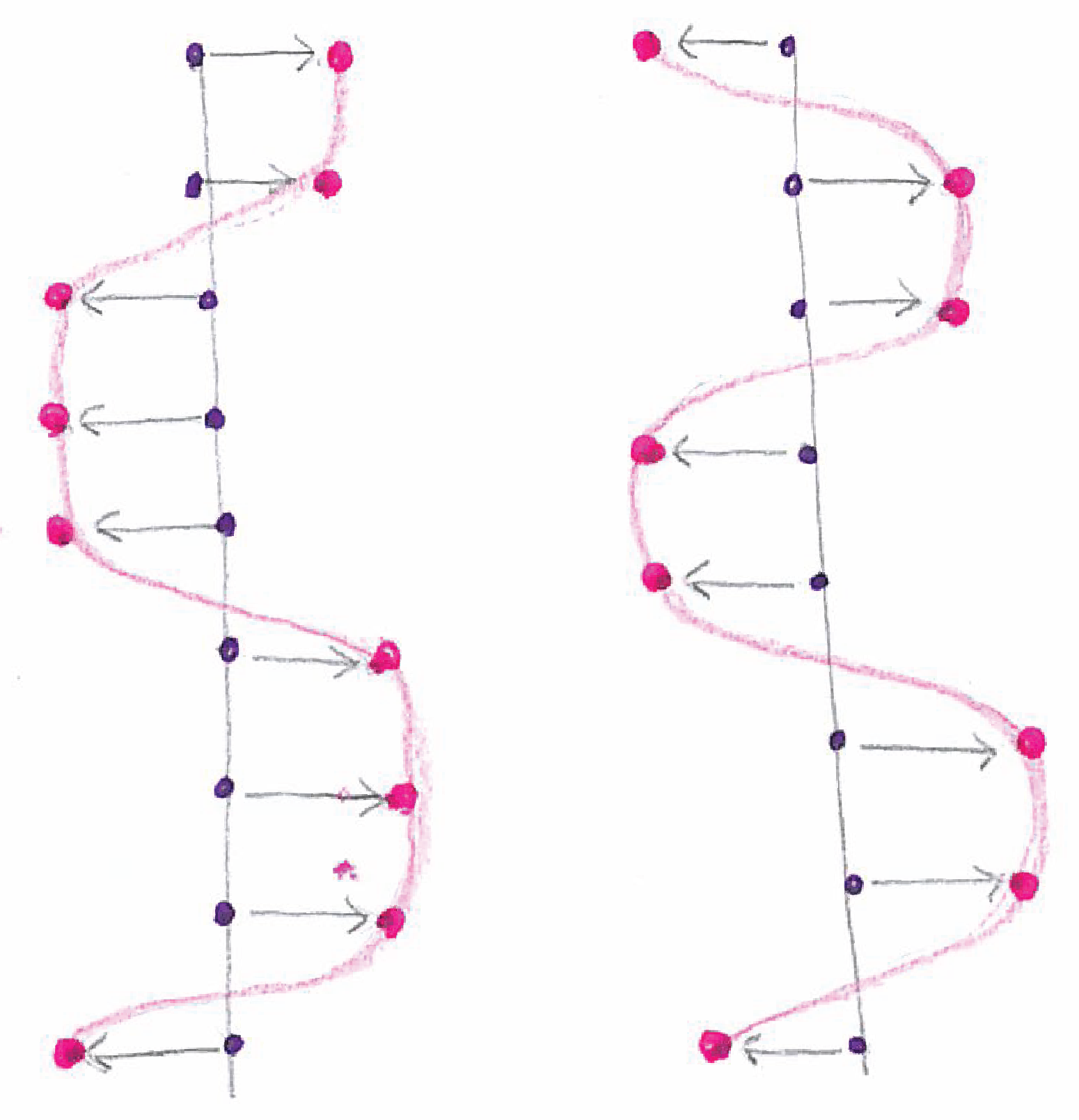
Version 2 (amplitude and undulating movement)¶

Parameters: points, amplitude, and bending pattern

The algorithm creates undulating movements passing every one, two, or three stripes, and so on. The undulating movement is defined by the bending pattern rule (this can include irregular patterns).

Double and triple space undulating patterns.	Irregular undulating patterns.

In [ ]:

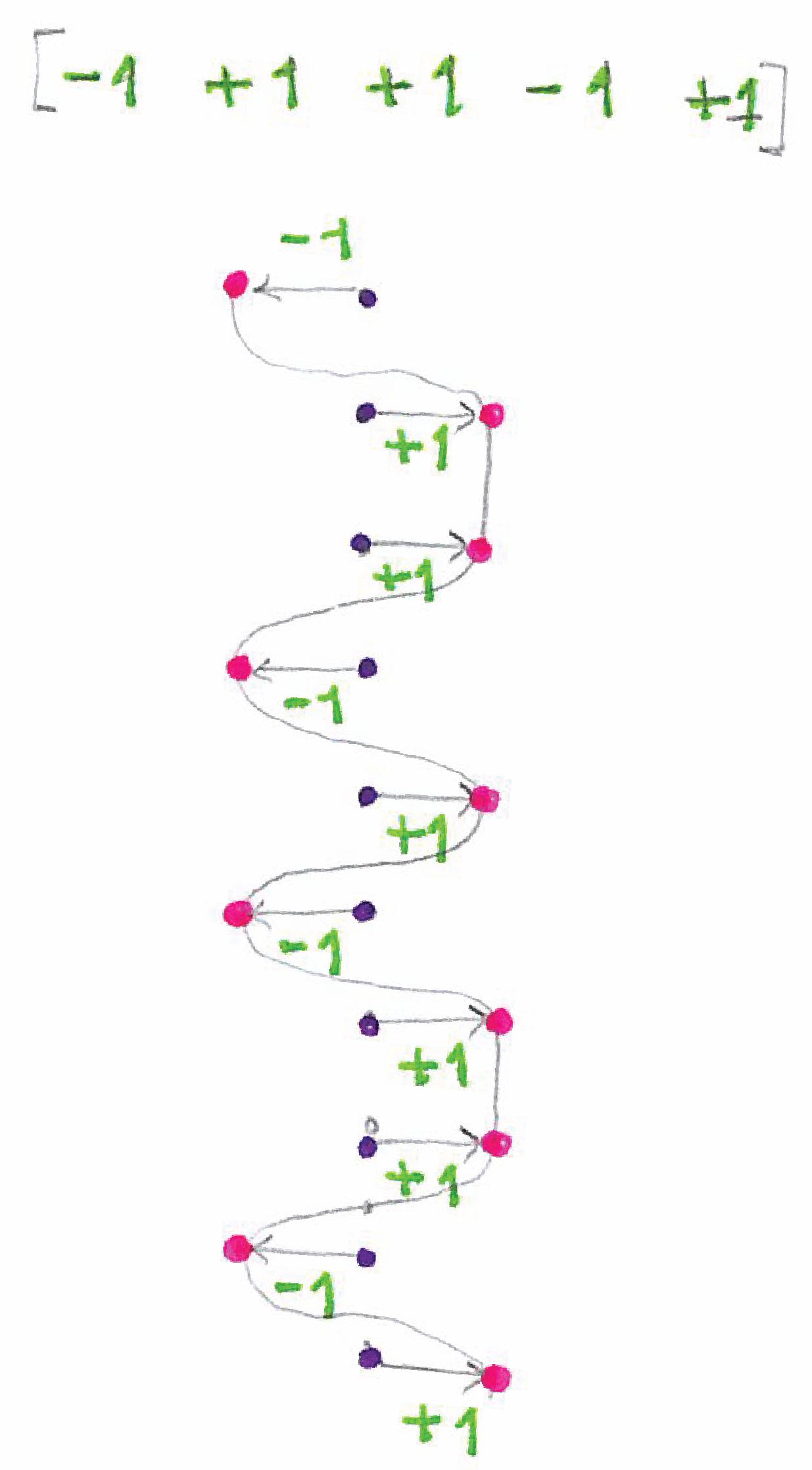stripe_2D_pts(pts, amp, bending_pattern) =
    [let p1 = pt1 + up_or_down*vy(amp),
         p2 = pt2 + next_up_or_down*vy(amp)
      [p1, intermediate_loc(p1, p2, 0.5)]
     end
     for (pt1, pt2, up_or_down, next_up_or_down)
     in zip(pts,
            [pts[2:end]...,pts[end]],
            cycle(bending_pattern),
            cycle([bending_pattern[2:end]...,bending_pattern[1]]))]

Test stripe_2D_pts function. The expected results are 2D splines with different undulating movements.

In [ ]:

@test begin
    
new_backend()

@manipulate for amp0=widget(0:0.01:1, label="Spline1 Amplitude"),
                amp1=widget(0:0.01:1, label="Spline2 Amplitude"),
                amp2=widget(0:0.01:1, label="Spline3 Amplitude"),
                amp3=widget(0:0.01:1, label="Spline4 Amplitude")
                delete_all_shapes()
        
                pts = ptss[2]
                spline(vcat(stripe_2D_pts(pts, amp0, [+1,-1])...)[1:end-1])
    
                pts = ptss[3]
                spline(vcat(stripe_2D_pts(pts, amp1, [+1,+1,-1,-1])...)[1:end-1])
    
                pts = ptss[4]
                spline(vcat(stripe_2D_pts(pts, amp2, [+1,+1,+1,-1,-1])...)[1:end-1])

                pts = ptss[5]
                spline(vcat(stripe_2D_pts(pts, amp3, [+1,+1,-1,-1,-1,-1])...)[1:end-1])
                nothing
            end
    
end

Expected result:

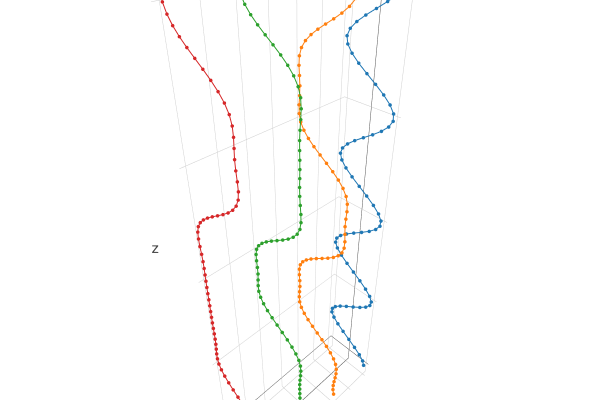
Version 3 (amplitude, undulating movement, and undulating direction)¶

Parameters: points, amplitude, bending pattern, and normal vectors

This version of the algorithm adapts to any plan or surface. The additional argument describes the direction in which each point should move. nvs_stripe should be an array of vector functions.

Normal vectors.

In [ ]:

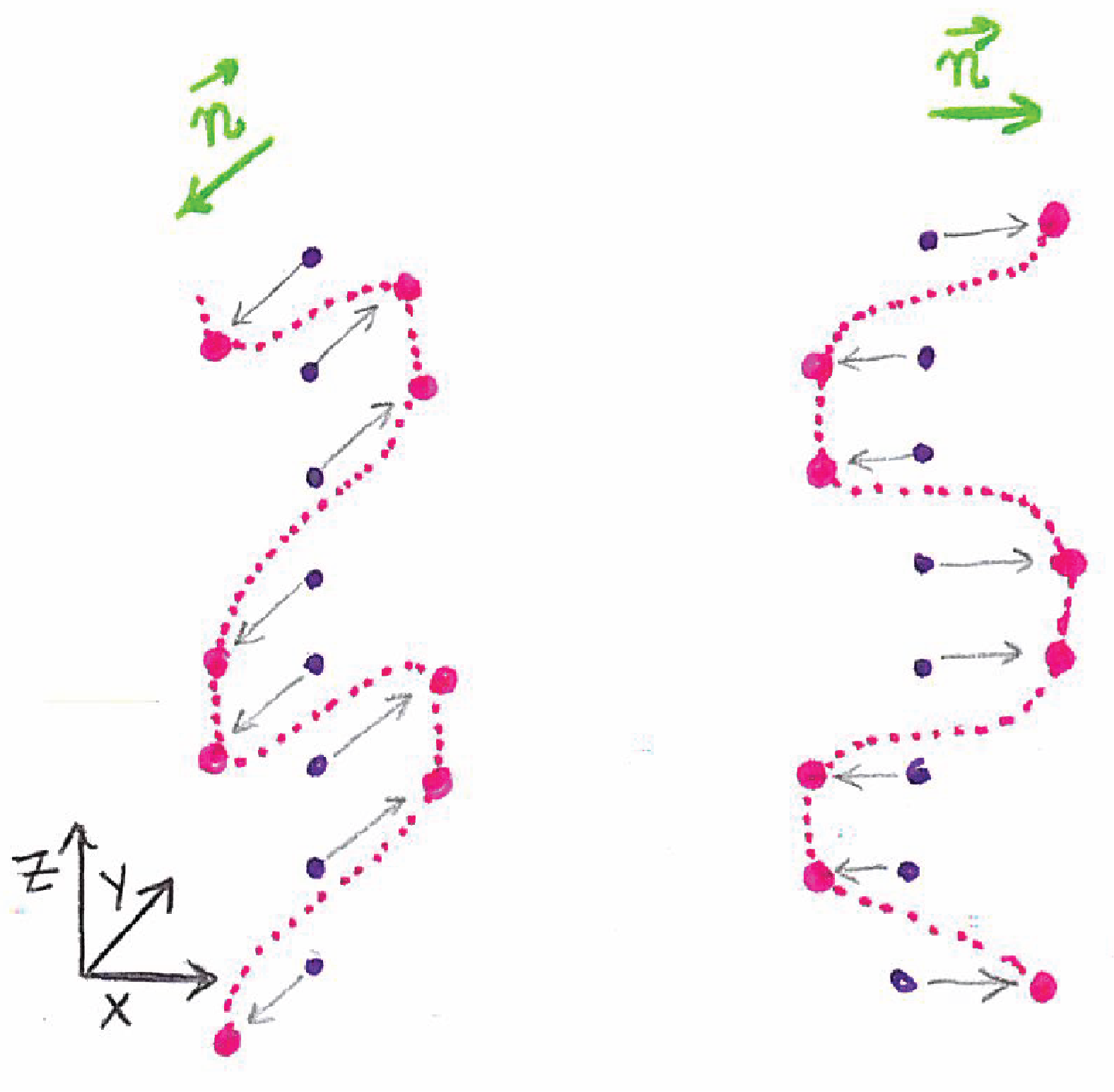stripe_2D_pts(pts, amp, bending_pattern, nvs_stripe) =
    [let p1 = pt1 + nv*up_or_down*amp,
         p2 = pt2 + nv*next_up_or_down*amp
      [p1, intermediate_loc(p1, p2, 0.5)]
     end
     for (pt1, pt2, nv, up_or_down, next_up_or_down)
     in zip(pts,
            [pts[2:end]...,pts[end]],
            nvs_stripe,
            cycle(bending_pattern),
            cycle([bending_pattern[2:end]...,bending_pattern[1]]))]

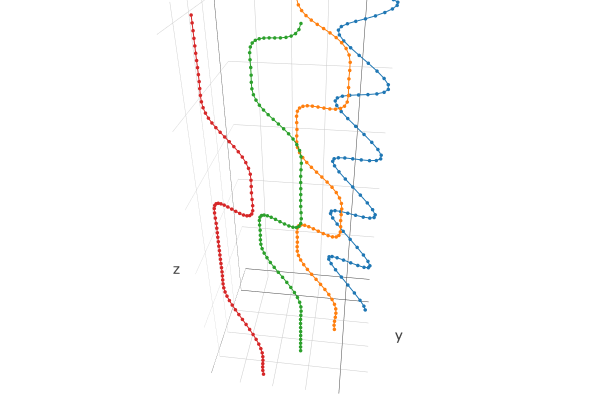
Test stripe_2D_pts function. The expected results are 2D splines oriented according to different normal vectors.

In [ ]:

@test begin
new_backend()

ptss = map_division((i,j)->xyz(i,i,j), 0, 10, 10, 0, 10, 10)
vss = normals_surface_extra_row(ptss)

pts = ptss[1]
vs = vss[1]
spline(vcat(stripe_2D_pts(pts, 1, [+1,-1], vs)...))

pts = ptss[2]
vs = vss[2]
spline(vcat(stripe_2D_pts(pts, 1, [+1,+1,-1,-1], vs)...)[1:end-1])

pts = ptss[3]
vs = vss[3]
spline(vcat(stripe_2D_pts(pts, 1, [+1,+1,+1,-1,-1], vs)...)[1:end-1])

pts = ptss[4]
vs = vss[4]
spline(vcat(stripe_2D_pts(pts, 1, [+1,+1,-1,-1,-1,-1], vs)...)[1:end-1])

end

Expected result:

Function that Creates the Axes of n Stripes in One of the Domain's Direction¶

Parameters: Points, amplitude, and the weave pattern.

two-dimensional distribution of points: matrix of points instead of an array of points
Stripes’ movement: all-ones matrix
Amplitude of the undulating movement
Normal vectors are calculated automatically
The output is another matrix of points containing the moved points

Matrix of points.	Weave pattern matrix.

Application of the stripe_2d_pts function.	Calculate normal vector.

In [ ]:

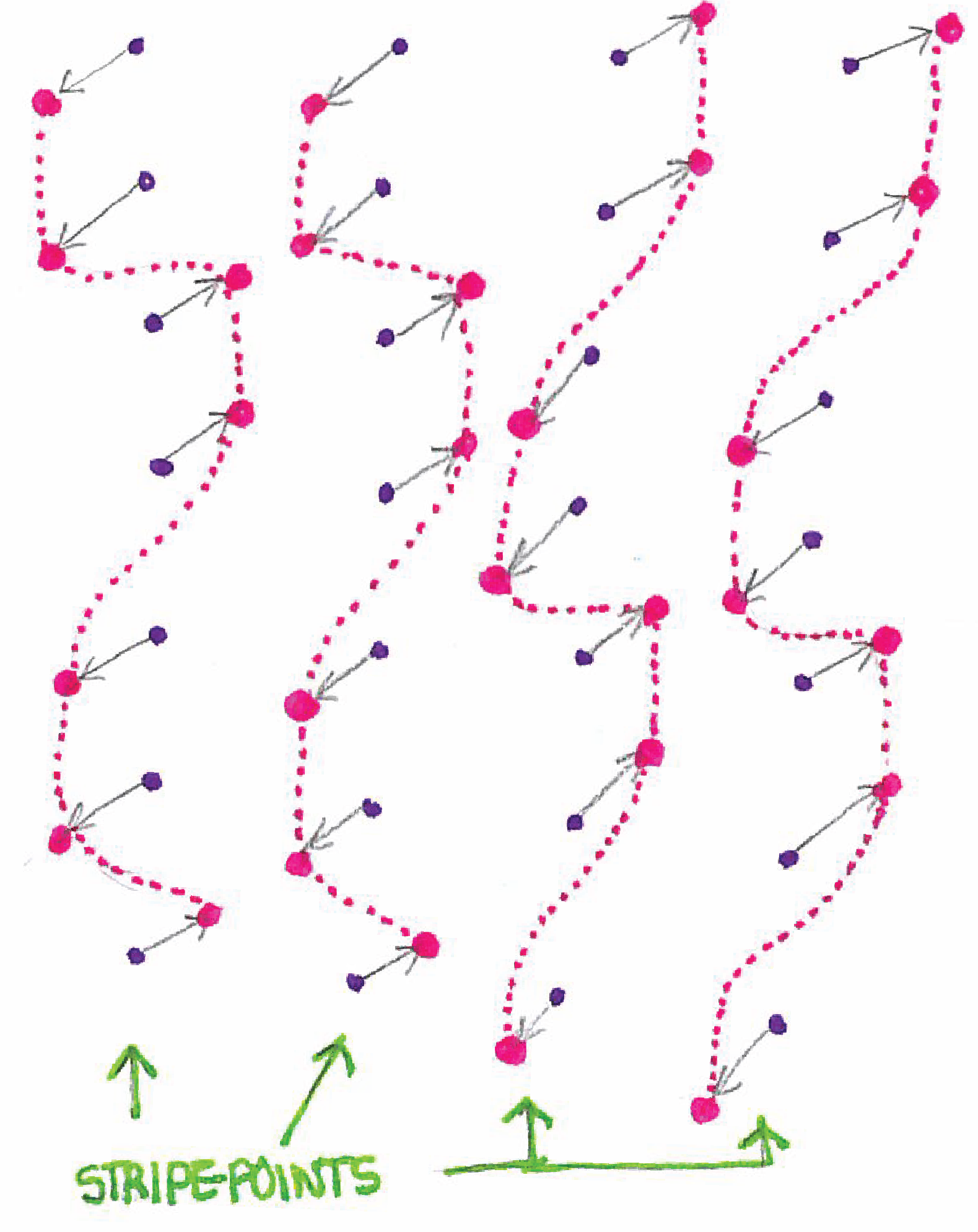stripes_2D_ptss(ptss, amp, weave_pattern)=
    let nvs = normals_surface_extra_row(ptss)
      [vcat(stripe_2D_pts(pts, amp, bending_pattern, nv_surf)...)[1:end-1]
       for (pts, nv_surf, bending_pattern) in zip(ptss, nvs, cycle(weave_pattern))]
    end

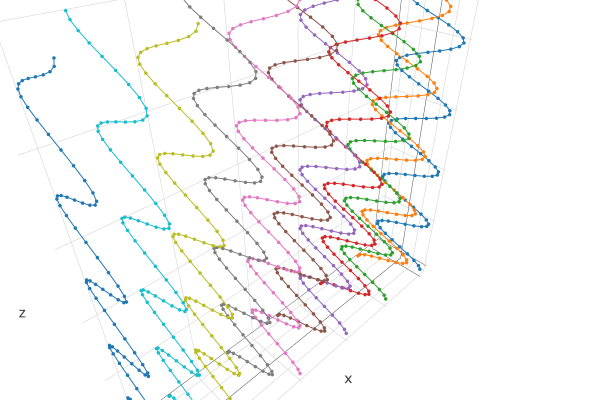
Test stripes_2D_ptss function. The expected result is a set of parallel splines representing a façade, using the weaving patterns shown below.

Weaving pattern examples.

In [ ]:

@test begin
new_backend()

ptss = map_division(xz, 0, 10, 10, 0, 10, 10)
map(i->spline(i), stripes_2D_ptss(ptss, 1, [[+1,-1],[-1,+1]]))
nothing
    
end

Expected result:

In [ ]:

@test begin
new_backend()

ptss = map_division(xz, 12, 22, 10, 0, 10, 10)
map(i->spline(i), stripes_2D_ptss(ptss, 1, [[+1,-1,-1],[-1,+1,+1]]))
nothing
    
end

Expected result:

In [ ]:

@test begin
new_backend()

ptss = map_division(xz, 24, 34, 10, 0, 10, 10)
map(i->spline(i), stripes_2D_ptss(ptss, 1, [[+1,-1,-1,-1],[-1,+1,+1,+1]]))
nothing
    
end

Expected result:

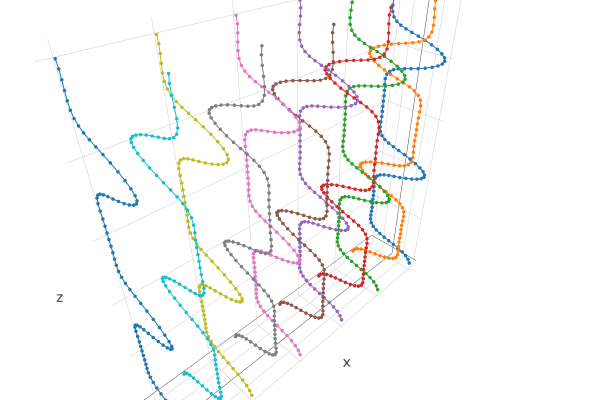
Function that Creates the Axes of n Stripes in Both Domain Directions¶

Produces n parallel undulating stripes in both domain’s directions
Ensures the stripes do not intersect each other: algorithm applies opposite movement

Domain, and domain sub-division.

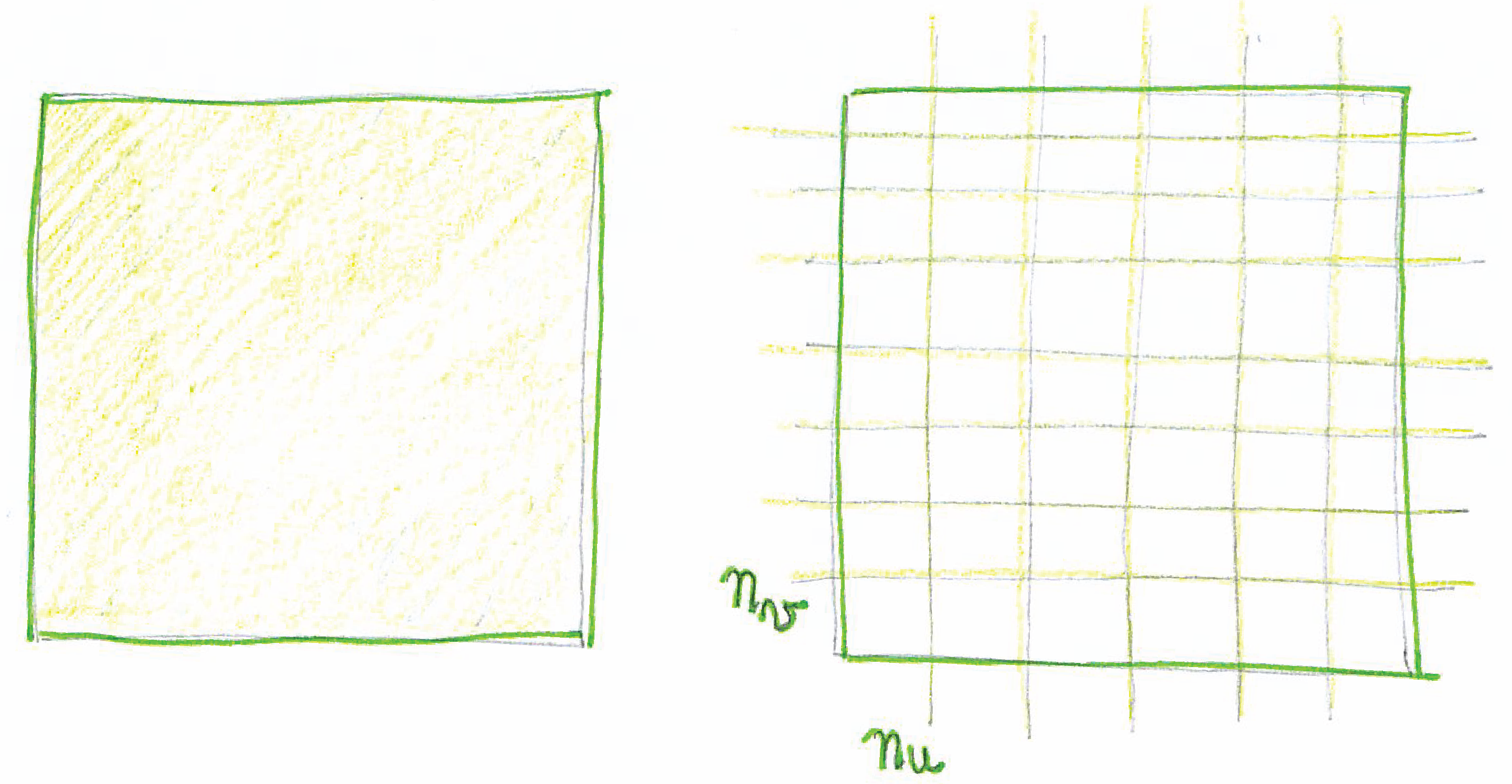Alternate movement at each intersection point.

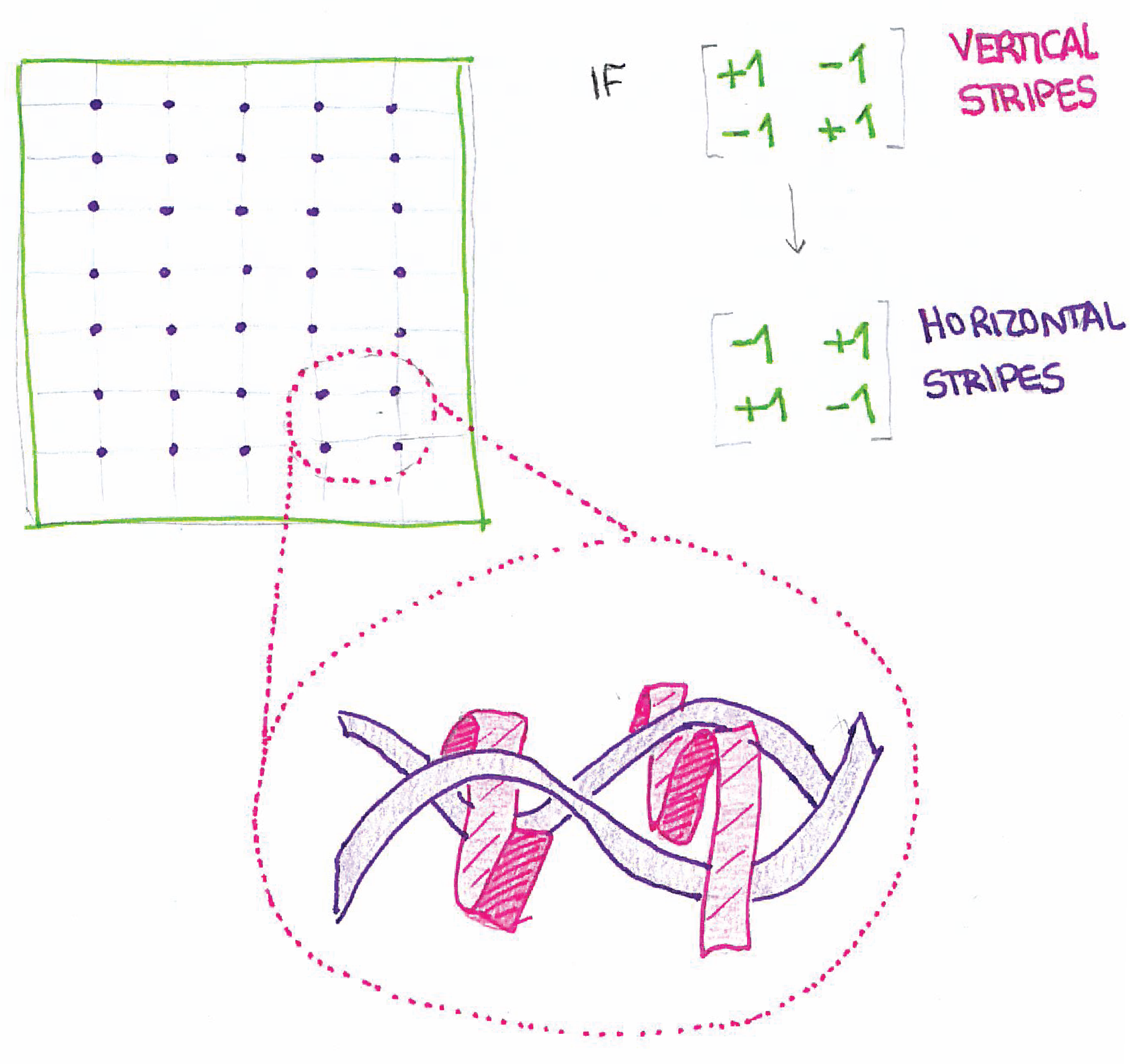Version 1 (different width values)¶

Parameters: matrix of points, number of stripes (vertical and horizontal), amplitude, weave pattern, and set of width values

Spatial surface defined by the matrix of points
Width values are used to center the stripes' axes
Width set should be composed of two arrays: vertical and horizontal values

Weaving with different stripe widths.

In [ ]:

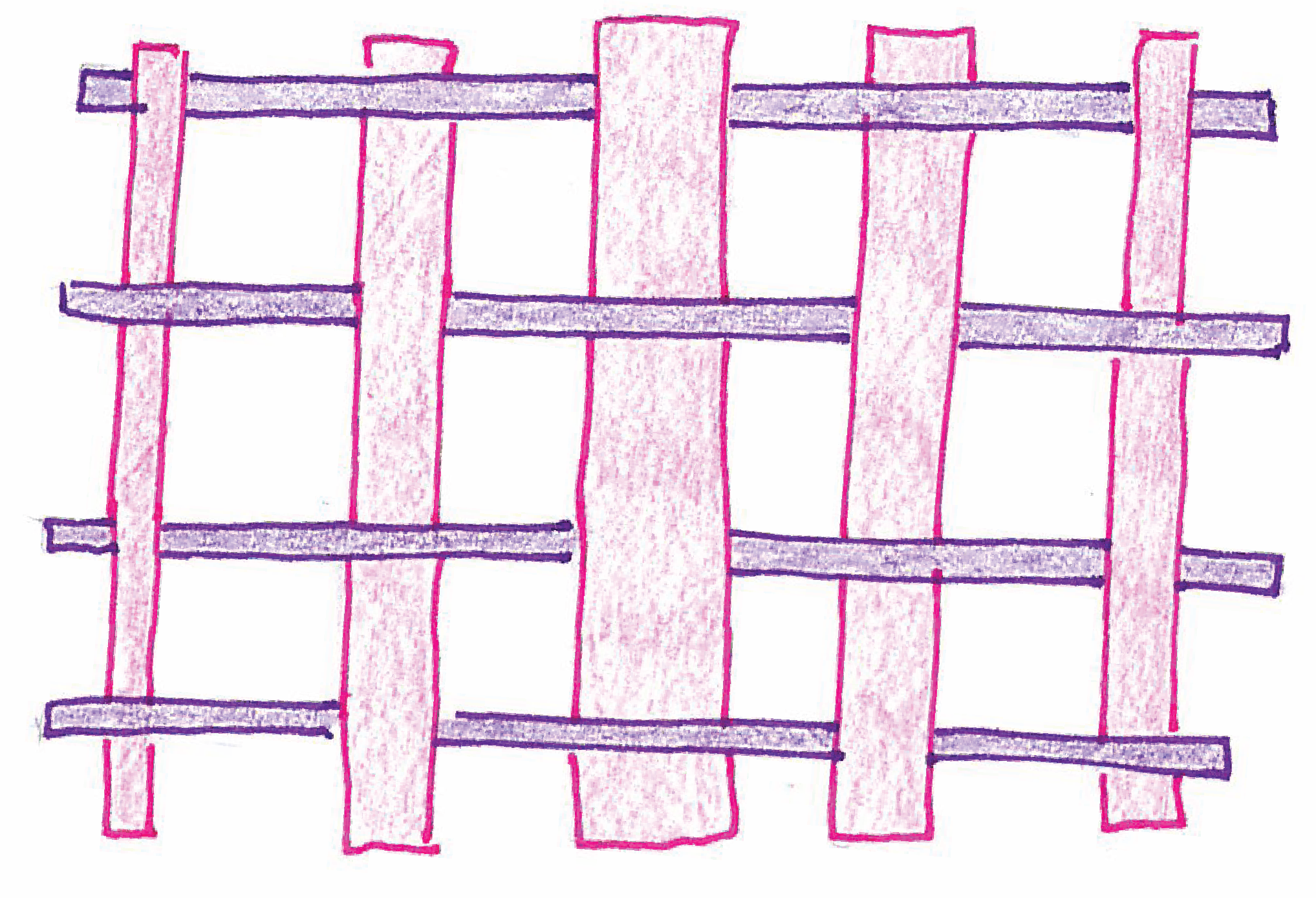weave_ptss_centered(s, nu, nv, amp, weave_pattern, stripes_widths) =
    let Δu_ini = maximum(stripes_widths[1])/2,
        Δv_ini = maximum(stripes_widths[2])/2,
        ptss_v = surf_pts(s.f, s.u0 + Δu_ini, s.u1 - Δu_ini, s.v0, s.v1, nu - 1, nv - 1),
        ptss_u = transpose_matrix(surf_pts(s.f, s.u0, s.u1, s.v0 + Δv_ini, s.v1 - Δv_ini, nu - 1, nv - 1)),
        inverse_weave_pattern = transpose_matrix(weave_pattern)
      [stripes_2D_ptss(ptss_v, amp, weave_pattern),
       stripes_2D_ptss(ptss_u, amp, inverse_weave_pattern)]
   end

Test weave_ptss_centered function. The expected result is a set of weaved splines.

In [ ]:

@test begin
new_backend()

facade = Surf((i,j)-> xz(i,j), 0, 10, 0, 10)

ptss = weave_ptss_centered(facade, 10, 10, 0.1, [[+1,-1],[-1,+1]], [[0.3], [0.3]])

map(i->spline(i), ptss[1])
map(i->spline(i), ptss[2])
nothing    
    
end

Expected result:

In [ ]:

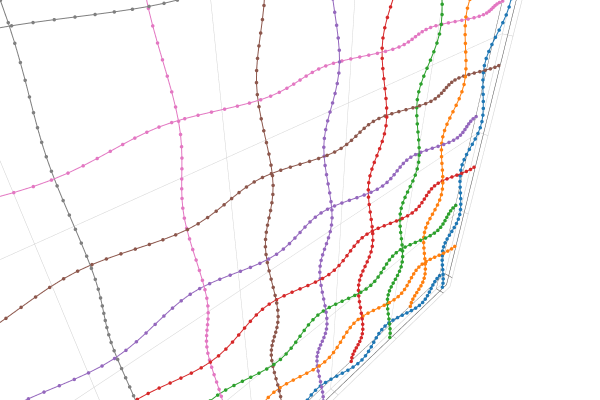
@test begin
new_backend()

facade = Surf((i,j)-> xz(i,j), 12, 22, 0, 10)

ptss = weave_ptss_centered(facade, 
                           10, 10, 0.1, 
                           [[+1,+1,-1,-1],
                            [-1,-1,+1,+1]], 
                           [[0.3], 
                            [0.3]])

map(i->spline(i), ptss[1])
map(i->spline(i), ptss[2])
nothing 
    
end

Expected result:

In [ ]:

@test begin
new_backend()

facade = Surf((i,j)-> xz(i,j), 24, 34, 0, 10)

ptss = weave_ptss_centered(facade, 
                           10, 10, 0.1,
                           [[+1,+1,+1,-1,-1],
                            [-1,-1,-1,+1,+1]],
                           [[0.3],
                            [0.3]])

map(i->spline(i), ptss[1])
map(i->spline(i), ptss[2])
nothing
    
end

Expected result:

Version 2 (straight verticals)¶

Parameters: matrix of points, number of stripes (vertical and horizontal), amplitude, weave pattern, set of width values, and a boolean value

Allow vertical stripes not to undulate -> structurally active elements
Use is_vertical_straight=true for static stripes

sketch 13

In [ ]:

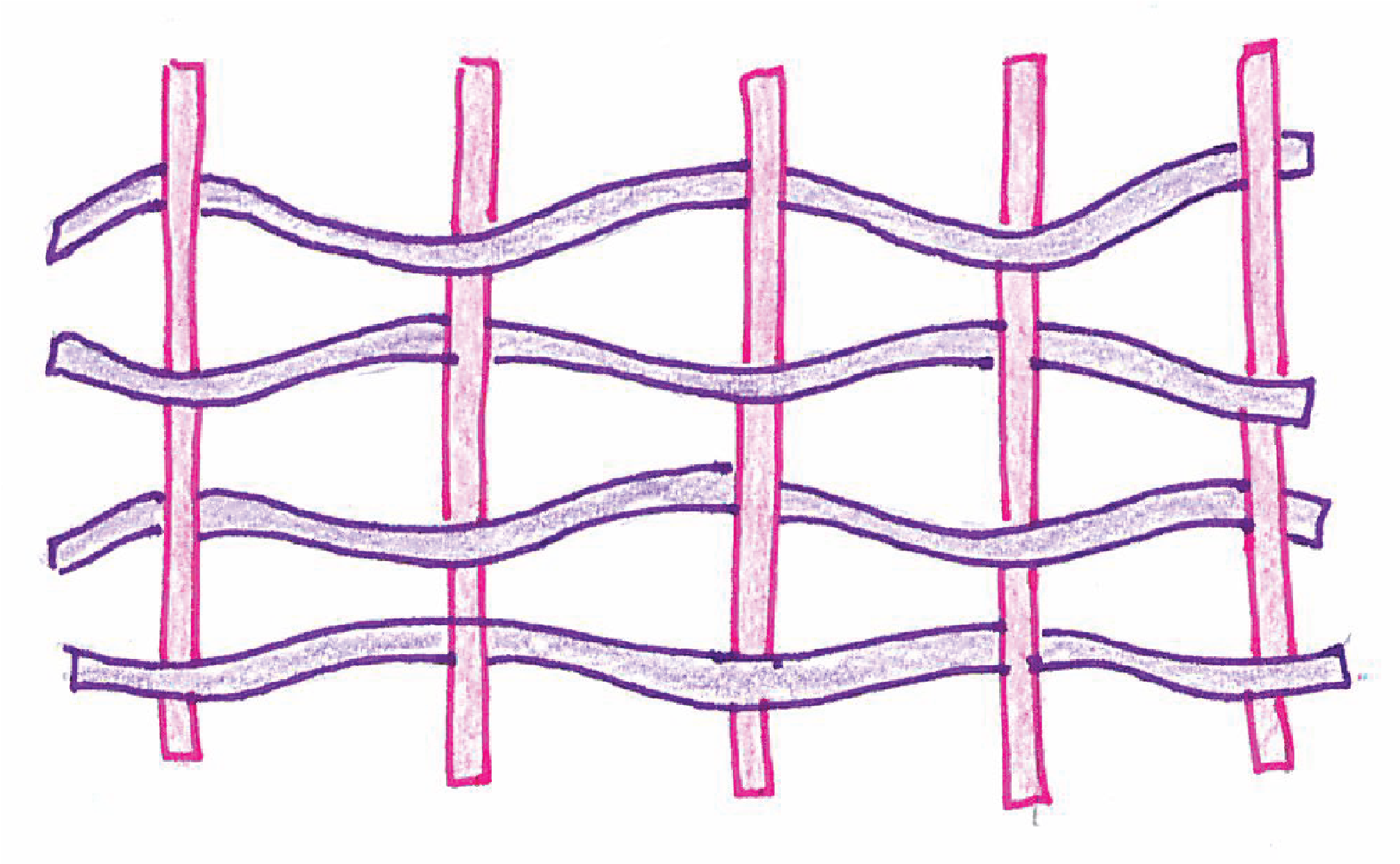weave_ptss_centered(s, nu, nv, amp, weave_pattern, stripes_widths,is_vertical_straight=false) =
    let Δu_ini = maximum(stripes_widths[1])/2,
        Δv_ini = maximum(stripes_widths[2])/2,
        ptss_v = surf_pts(s.f, s.u0 + Δu_ini, s.u1 - Δu_ini, s.v0, s.v1, nu - 1, nv - 1),
        ptss_u = transpose_matrix(surf_pts(s.f, s.u0, s.u1, s.v0 + Δv_ini, s.v1 - Δv_ini, nu - 1, nv - 1)),
        inverse_weave_pattern = transpose_matrix(weave_pattern),
        amp_v = is_vertical_straight ? 0 : amp
      [stripes_2D_ptss(ptss_v, amp_v, weave_pattern),
       stripes_2D_ptss(ptss_u, amp, inverse_weave_pattern)]
   end

Test weave_ptss_centered function. The expected result is a set of weaved splines with straight verticals.

In [ ]:

@test begin
new_backend()

facade = Surf((i,j)-> xz(i,j), 0, 10, 0, 10)

ptss = weave_ptss_centered(facade, 10, 10, 0.2, [[+1,-1],[-1,+1]], [[0.3], [0.3]], true)

map(i->spline(i), ptss[1])
map(i->spline(i), ptss[2])
nothing 
    
end

Expected result:

In [ ]:

@test begin
new_backend()

facade = Surf((i,j)-> xz(i,j), 12, 22, 0, 10)

ptss = weave_ptss_centered(facade, 10, 10, 0.2, [[+1,+1,-1,-1],[-1,-1,+1,+1]], [[0.3], [0.3]], true)

map(i->spline(i), ptss[1])
map(i->spline(i), ptss[2])
nothing  

end

Expected result:

In [ ]:

@test begin
new_backend()

facade = Surf((i,j)-> xz(i,j), 24, 34, 0, 10)

ptss = weave_ptss_centered(facade, 10, 10, 0.2, [[+1,+1,+1,-1,-1],[-1,-1,-1,+1,+1]], [[0.3], [0.3]], true)

map(i->spline(i), ptss[1])
map(i->spline(i), ptss[2])
nothing 
    
end

Expected result:

Version 3 (straight horizontals)¶

Parameters: matrix of points, number of stripes (vertical and horizontal), amplitude, weave pattern, set of width values, and two boolean values (vertical and horizontal)

Allow horizontal stripes not to undulate -> structurally active elements
Use is_horizotal_straight=true for static stripes

sketch 14

In [ ]:

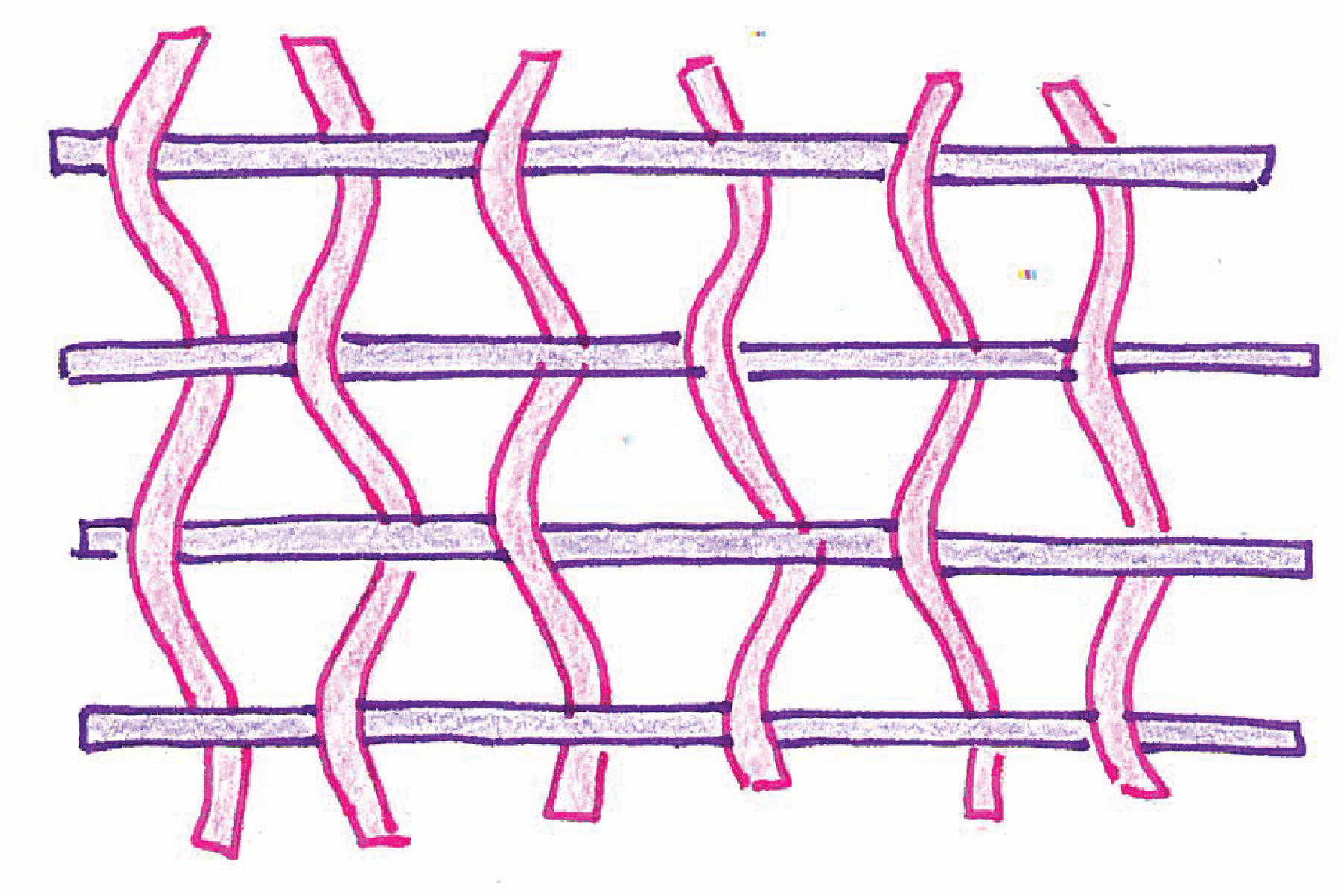weave_ptss_centered(s, nu, nv, amp, weave_pattern, stripes_widths,
                    is_vertical_straight=false, is_horizotal_straight=false) =
    let Δu_ini = maximum(stripes_widths[1])/2,
        Δv_ini = maximum(stripes_widths[2])/2,
        ptss_v = surf_pts(s.f, s.u0 + Δu_ini, s.u1 - Δu_ini, s.v0, s.v1, nu - 1, nv - 1),
        ptss_u = transpose_matrix(surf_pts(s.f, s.u0, s.u1, s.v0 + Δv_ini, s.v1 - Δv_ini, nu - 1, nv - 1)),
        inverse_weave_pattern = transpose_matrix(weave_pattern),
        amp_v = is_vertical_straight ? 0 : amp,
        amp_u = is_horizotal_straight ? 0 : amp
      [stripes_2D_ptss(ptss_v, amp_v, weave_pattern),
       stripes_2D_ptss(ptss_u, amp_u, inverse_weave_pattern)]
   end

Test weave_ptss_centered function. The expected result is a set of weaved splines with straight horizontals.

In [ ]:

@test begin 
new_backend()

facade = Surf((i,j)-> xz(i,j), 0, 10, 0, 10)

ptss = weave_ptss_centered(facade, 10, 10, 0.2, [[+1,-1],[-1,+1]], [[0.3], [0.3]], false, true)

map(i->spline(i), ptss[1])
map(i->spline(i), ptss[2])
nothing

end

Expected result:

In [ ]:

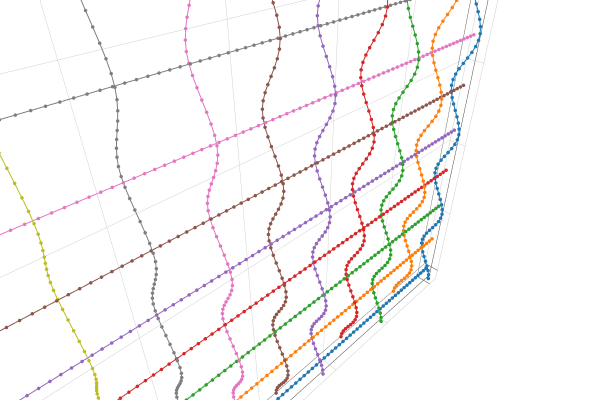
@test begin 
new_backend()

facade = Surf((i,j)-> xz(i,j), 12, 22, 0, 10)

ptss = weave_ptss_centered(facade, 10, 10, 0.2, [[+1,+1,-1,-1],[-1,-1,+1,+1]], [[0.3], [0.3]], false, true)

map(i->spline(i), ptss[1])
map(i->spline(i), ptss[2])
nothing
    
end

Expected result:

In [ ]:

@test begin 
new_backend()

facade = Surf((i,j)-> xz(i,j), 24, 34, 0, 10)

ptss = weave_ptss_centered(facade, 10, 10, 0.2, [[+1,+1,+1,-1,-1],[-1,-1,-1,+1,+1]], [[0.3], [0.3]], false, true)
nothing

map(i->spline(i), ptss[1])
map(i->spline(i), ptss[2])
nothing
    
end

Expected result:

Function that Creates a Stripe¶

Materializes the stripes to a physical elements, with the appropriate width and thickness.

In [ ]:

backend(meshcat)

In [ ]:

Khepri.meshcat_material(color) =
  (uuid=string(Khepri.uuid1()),
   type="MeshLambertMaterial",
   side=2,
   color="0x$(Khepri.hex(color))",
   emissive="0x$(Khepri.hex(color))",
   emissiveIntensity=0.2)

In [ ]:

vertical=create_layer("vertical", true, RGB(211/255, 146/255, 212/255))
horizontal=create_layer("horizontal", true, RGB(124/255, 70/255, 156/255))
nothing

Version 1 (materialize stripe)¶

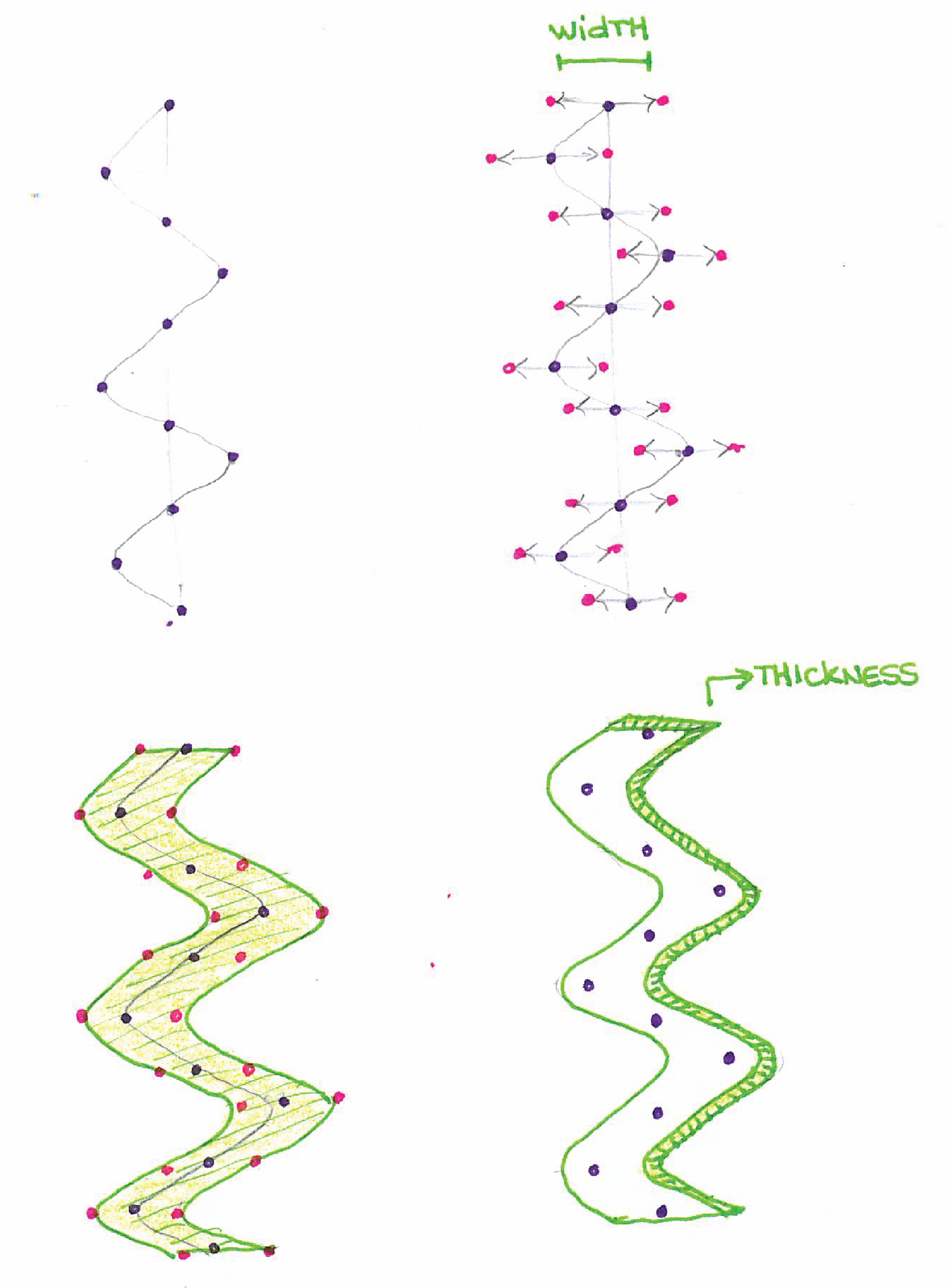
Parameters: points, stripe width, and thickness

Calculate the points delimiting the contour of the stripe
Materialize those points in the form of a surface with the desired thickness

Materializing a stripe.

In [ ]:

smooth_pts(pts) = map_division(in_world, open_spline_path(pts), 50)

In [ ]:

smooth_surface_grid(ptss)=surface_grid(smooth_pts.(ptss))

In [ ]:

stripe_centered(pts, stripe_width, stripe_thick) =
    with(current_layer, vertical) do    
        thicken(
            smooth_surface_grid([map(pt-> pt-vpol(stripe_width/2, 0), pts),
                          map(pt-> pt+vpol(stripe_width/2, 0), pts)]),
            stripe_thick)
        end

Test stripe_centered function. The expected result is a stripe.

In [ ]:

@test begin
new_backend()
set_view(xyz(7.229,6.523,0.167), u0(), 20)

facade = Surf((i,j)-> xz(i,j-5), 0, 10, 0, 10)

ptss = weave_ptss_centered(facade, 10, 10, 0.2, [[+1,-1],[-1,+1]], [[0.3], [0.3]], false, true)
stripe_centered(ptss[1][1], 0.3, 0.01)

ptss = weave_ptss_centered(facade, 10, 10, 0.2, [[+1,-1,-1],[-1,+1,+1]], [[0.3], [0.3]], false, true)
stripe_centered(ptss[1][2], 0.3, 0.01)

ptss = weave_ptss_centered(facade, 10, 10, 0.2, [[+1,+1,-1,-1,-1],[-1,-1,+1,+1,+1]], [[0.3], [0.3]], false, true)
stripe_centered(ptss[1][3], 0.3, 0.01)

ptss = weave_ptss_centered(facade, 10, 10, 0.2, [[+1,-1,-1,-1,-1],[-1,+1,+1,+1,+1]], [[0.3], [0.3]], false, true)
stripe_centered(ptss[1][4], 0.3, 0.01)
    
end

Expected result:

Version 2 (scale factor)¶

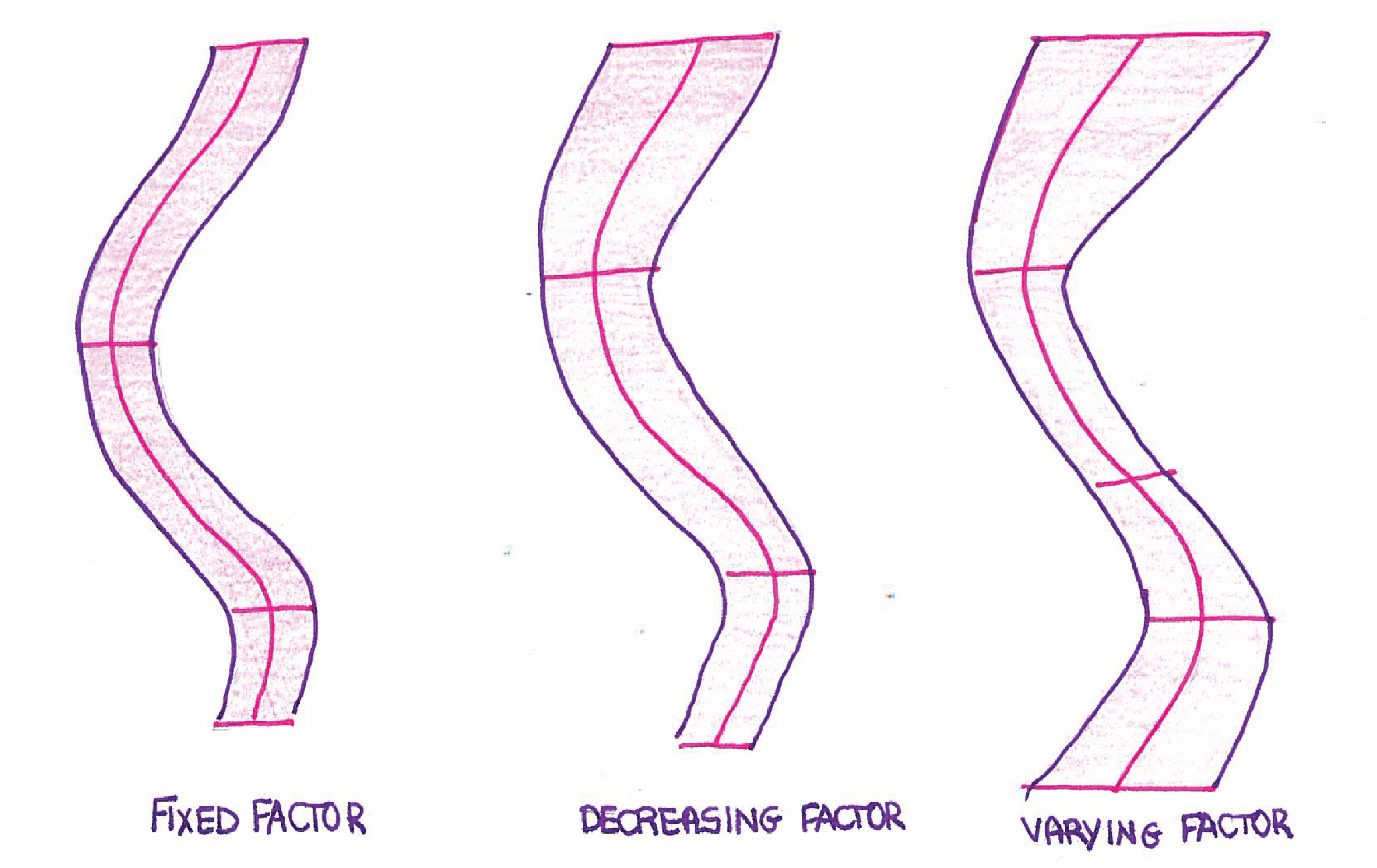
Parameters: points, stripe width and thickness, and width scale function

In case the width scale function returns a constant value of 1, the stripe's width never changes
Otherwise, the width varies according to the factor received, being 0 the minimum and 1 the maximum possible values

Stripe width variation.

In [ ]:

stripe_centered(pts, stripe_width, stripe_thick, f_width) =
    with(current_layer, vertical) do  
        thicken(
            smooth_surface_grid([map(pt-> pt-vpol(stripe_width/2 + f_width(pt), 0), pts),
                          map(pt-> pt+vpol(stripe_width/2 + f_width(pt), 0), pts)]),
                stripe_thick)
    end

Test stripe_centered function. The expected results are stripes with varying widths.

In [ ]:

@test begin
new_backend()
set_view(xyz(7.229,6.523,0.167), u0(), 20)
    
facade = Surf((i,j)-> xz(i,j-5), 0, 10, 0, 10)

ptss = weave_ptss_centered(facade, 10, 10, 0.2, [[+1,-1],[-1,+1]], [[0.3], [0.3]], false, true)

stripe_centered(ptss[1][1], 0.3, 0.01, i->sin(i.z/pi/4))

stripe_centered(ptss[1][3], 0.3, 0.01, i->sin(pi/2+i.z/pi/2)) 

stripe_centered(ptss[1][5], 0.3, 0.01, i->sin(i.z/pi))

stripe_centered(ptss[1][7], 0.3, 0.01, i->0.5*abs(sin(i.z*2pi)))
    
end

Expected result:

Version 3 (rotation)¶

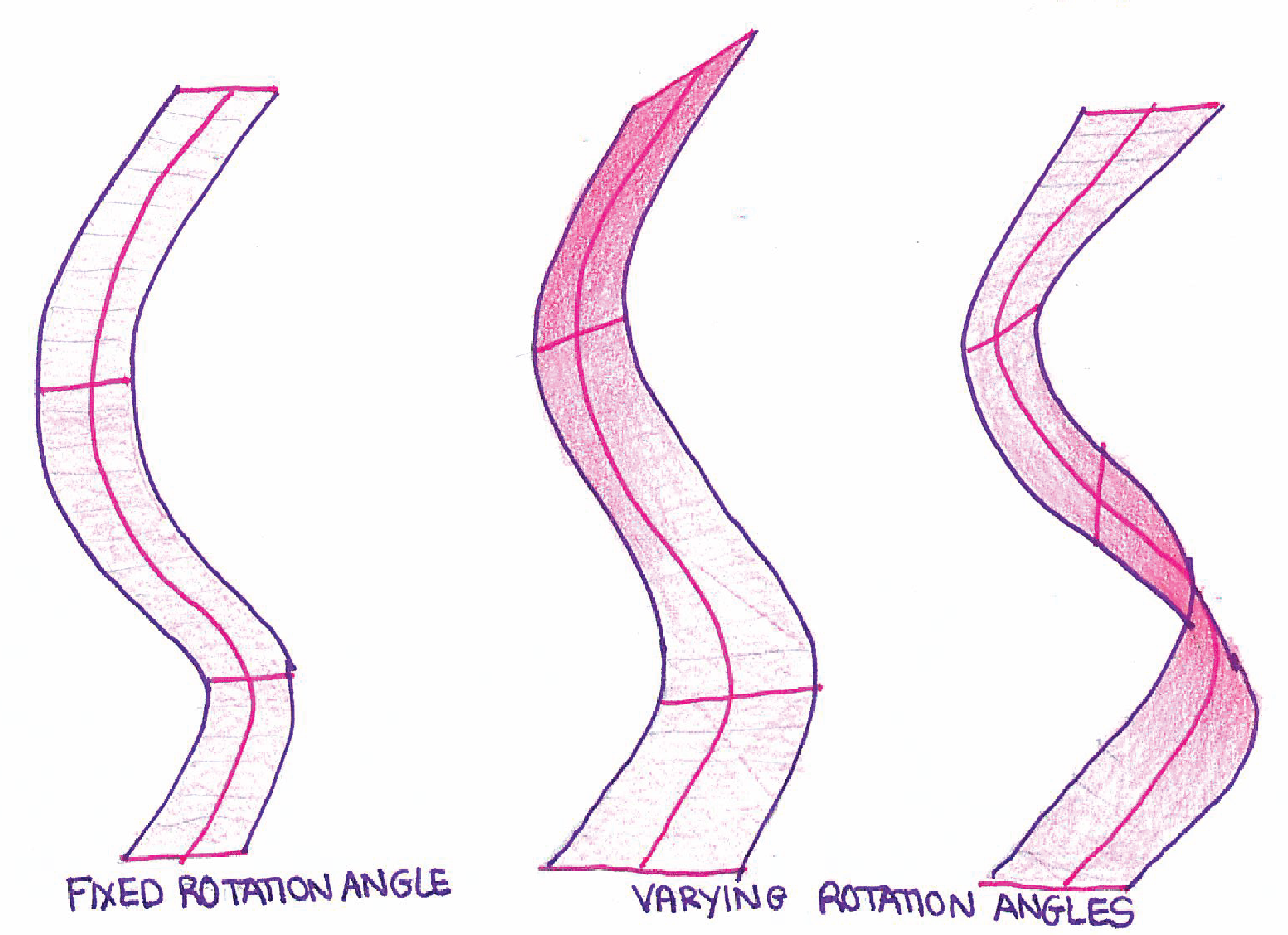
Parameters: points, stripe width and thickness, width scale function, and rotation function

In case the rotation function returns a constant value of 1, the stripe's angle does not change.
Otherwise, the rotation varies according to the factor received, being 0 the minimum and 1 the maximum possible values.

Stripe rotation.

In [ ]:

stripe_centered(pts, stripe_width, stripe_thick, f_width, f_rotations) =
        thicken(
            smooth_surface_grid([map(pt-> pt-vpol(stripe_width/2 + f_width(pt), f_rotations[1](pt)), pts),
                          map(pt-> pt+vpol(stripe_width/2 + f_width(pt), f_rotations[2](pt)), pts)]),
                stripe_thick)

Test stripe_centered function. The expected results are stripes with varying widths and rotations.

The following expression represents the rotation function used in the first example.

$$ S_{rotation} = \frac{\pi}{ 2} \times \left (-1 + cos\left (2 \pi \times \frac{cz\left ( i \right )}{10} \right ) \right ) $$

In [ ]:

@test begin   
new_backend()
set_view(xyz(7.229,6.523,0.167), u0(), 20)

facade = Surf((i,j)-> xz(i,j-5), 0, 10, 0, 10)

ptss = weave_ptss_centered(facade, 10, 10, 0.2, [[+1,-1],[-1,+1]], [[0.3], [0.3]], false, true)

with(current_layer, vertical) do  
    stripe_centered(ptss[1][1], 0.3, 0.01, i->sin(i.z/pi/4),
                    [i->pi/2*(-1+cos(2pi*i.z/10)),
                     i->pi/2*(-1+cos(2pi*i.z/10))])

    stripe_centered(ptss[1][3], 0.3, 0.01, i->sin(i.z/pi/4),
                    [i->pi*(-1+cos(2pi*i.z/10)),
                     i->pi*(-1+cos(2pi*i.z/10))])

    stripe_centered(ptss[1][5], 0.3, 0.01, i->sin(i.z/pi/4),
                    [i->pi/4*(-1+cos(2pi*i.z/10)),
                     i->pi/4*(-1+cos(2pi*i.z/10))])

    stripe_centered(ptss[1][7], 0.3, 0.01, i->sin(i.z/pi/4),
                    [i->pi/4*(-1+cos(pi*i.z/10)),
                     i->pi/4*(-1+cos(pi*i.z/10))])
end
    
end

Expected result:

Function that Creates Interweaved Stripes¶

Parameters: points, stripes width and thickness, width, and rotation functions

points = array of weaving spatial locations -> output of the weaved_ptss_centered
Creates stripes with given widths, thicknesses and rotations (horizontally and vertically)
If stripe width = 0, no stripe is created

Weaving spatial locations and resulting stripes.

Null stripe example.

In [ ]:

stripes_with_rotation(ptss, stripes_widths, thickness, f_widths, f_rotations) =
    vcat([width==0 ? empty_shape() :
        with(current_layer, vertical) do
            stripe_centered(pt, width, thickness[1], f_widths[1], f_rotations[1])
        end
        for (pt,width) in zip(ptss[1], cycle(stripes_widths[1]))],
            with(current_cs, cs_from_o_vx_vy(u0(), vz(1), vy(1))) do
                [width==0 ? empty_shape() :
                    with(current_layer, horizontal) do
                        stripe_centered(pt, width, thickness[2], f_widths[2], f_rotations[2])
                    end
                for (pt,width) in zip(ptss[2], cycle(stripes_widths[2]))]
            end
        )

Test stripes_with_rotation function. The expected result is a regular chess weaved façade.

In [ ]:

@test begin
new_backend()
set_view(xyz(8.881,6.913,0.338), u0(), 20)
    
facade = Surf((i,j)-> xz(i-5,j-5), 0, 10, 0, 10)

ptss = weave_ptss_centered(facade, 10, 10, 0.1, [[-1,+1],[+1,-1]], [[0.1],[0.1]], false, false)


stripes_with_rotation(ptss,
                       [[0.25],[0.25]],
                        [0.05, 0.05],
                        [i->0, i->0],
                        [[i->0,i->0],
                         [i->0,i->0]])
    
nothing
    
end

Expected result:

Test stripes_with_rotation function. The expected result is an irregular pattern weaved façade.

In [ ]:

@test begin
new_backend()
set_view(xyz(8.881,6.913,0.338), u0(), 20)    
    
facade = Surf((i,j)-> xz(i-5,j-5), 0, 10, 0, 10)

ptss = weave_ptss_centered(facade, 10, 10, 0.1, [[-1,+1,+1,+1],[+1,-1,+1,+1],[+1,+1,-1,+1],[+1,+1,+1,-1]], [[0.1],[0.1]], false, false)
nothing

stripes_with_rotation(ptss,
                      [[0.25],[0.25]],
                      [0.05, 0.05],
                      [i->0, i->0],
                      [[i->0,i->0],
                       [i->0,i->0]])
nothing
  
end

Expected result:

Test stripes_with_rotation function. The expected result is an irregular weaved façade with rotated horizontal stripes.

In [ ]:

@test begin
new_backend()
set_view(xyz(8.881,6.913,0.338), u0(), 20)
      
facade = Surf((i,j)-> xz(i-5,j-5), 0, 10, 0, 10)

ptss = weave_ptss_centered(facade, 10, 10, 0.2, [[-1,+1,+1,+1],[+1,-1,+1,+1],[+1,+1,-1,+1],[+1,+1,+1,-1]], [[0.1],[0.1]], false, false)

stripes_with_rotation(ptss,
                      [[0.25],[0.25]],
                      [0.05, 0.05],
                      [i->0, i->0],
                      [[i->0,i->0],
                       [i->pi/2*(-1+cos(2pi*i.x/10)),
                       i->pi/2*(-1+cos(2pi*i.x/10))]])
nothing
    
end

Expected result:

Test stripes_with_rotation function. The expected result is an irregular weaved façade with rotated vertical stripes.

In [ ]:

@test begin
new_backend()
set_view(xyz(8.881,6.913,0.338), u0(), 20)
    
facade = Surf((i,j)-> xz(i-5,j-5), 0, 10, 0, 10)

ptss = weave_ptss_centered(facade, 10, 10, 0.2, [[-1,+1,+1,+1],[+1,-1,+1,+1],[+1,+1,-1,+1],[+1,+1,+1,-1]], [[0.1],[0.1]], false, false)

stripes_with_rotation(ptss,
                      [[0.25],[0.25]],
                      [0.05, 0.05],
                      [i->0, i->0],
                      [[i->pi/2*(-1+cos(2pi*i.z/10)),
                       i->pi/2*(-1+cos(2pi*i.z/10))],
                       [i->0,i->0]])
nothing
    
end

Expected result:

Test stripes_with_rotation function. The expected result is an irregular weaved façade with varying widths.

In [ ]:

@test begin
new_backend()
set_view(xyz(8.881,6.913,0.338), u0(), 20)
    
facade = Surf((i,j)-> xz(i-5,j-5), 0, 10, 0, 10)

ptss = weave_ptss_centered(facade, 10, 10, 0.2, [[-1,+1,+1,+1],[+1,-1,+1,+1],[+1,+1,-1,+1],[+1,+1,+1,-1]], [[0.1],[0.1]], false, false)
nothing

stripes_with_rotation(ptss,
                      [[0.1],[0.1]],
                      [0.05, 0.05],
                      [i->0.05+0.4*sin(i.z/pi/4), i->0.05+0.1*sin((i.x-48)/pi)],
                      [[i->0,i->0],[i->0,i->0]])
    
nothing

end

Expected result:

Test stripes_with_rotation function. The expected result is an irregular weaved façade with rotated stripes and varying widths.

In [ ]:

@test begin
new_backend()
set_view(xyz(8.881,6.913,0.338), u0(), 20)
    
facade = Surf((i,j)-> xz(i-5,j-5), 0, 10, 0, 10)

ptss = weave_ptss_centered(facade, 10, 10, 0.4, [[-1,+1,+1,+1],[+1,-1,+1,+1],[+1,+1,-1,+1],[+1,+1,+1,-1]], [[0.1],[0.1]], false, false)

stripes_with_rotation(ptss,
                      [[0.1],[0.1]],
                      [0.05, 0.05],
                      [i->0.4*sin(i.z/pi/4), i->0.09*sin((i.x-60)/pi)],
                      [[i->pi/2*(-1+cos(pi*i.z/10)),
                       i->pi/2*(-1+cos(pi*i.z/10))],
                       [i->0,i->0]])
    
nothing
    
end

Expected result:

Optimization¶

For the optimization, we designed a test cell represeting a typical office, where the south and east façade consit of a curtain wall overllaped with the weaved façade, we developed previous, to shade the interior space.

The two metrics involved in the optimization were spatial Daylight Autonmy (sDA) and Annual Sun Exposure (ASE), and the objectives were:

$$ minimize-f(x_1, x_2, x_3) = ASE_{1000,250h}(x_1, x_2, x_3)\\ maximize-g(x_1, x_2, x_3) = sDA_{300|50\%} (x_1, x_2, x_3) $$

x₁, x₂, and x₃ are the variables for our oprimization problem, representing: horizontal stripes number x₁ ∈ {6,7,…,20}, South horizontal stripes rotation x₂ ∈ {-π, -π + 0.02,…, π}, and East horizontal stripes width reduction factor x₃ ∈ {0, 0.02,…, 1.6}. The range of x₃ results from a periodic non-linear function with a sinusoid behavior wherein 0 means no change, and 1.6 means maximum width reduction.

Finally, we tested optimization three algorithms, NSGA-II, OMOPSO, and GPR_SPEA2. Each algorithm analyzed 400 solutions grouped in populations or swarms of 20.

Global Setup for Processing Data¶

In this section, we define all the global constants that will be used for the optimization.

In [ ]:

# Folders Structure
base_folder = pwd()
results_folder_phase1 = joinpath(base_folder, "algorithms")

# CSV File Configuration
has_header = true
files_sep = ","
file_extension = "csv"

# Optimization Settings
runs = [1]
nruns = length(runs)
max_evals = 500

## Problem Definition (in the files) 
### Variables
m_stripes = :m_stripes
rotation = :rotation
thickness = :thickness
vars_cols = [m_stripes, rotation, thickness]

### Objectives  
ASE = :ASE
sDA = :sDA
objs_cols = [ASE, sDA]

relevant_cols = vcat(vars_cols, objs_cols)

names_mapping = (
     4 => m_stripes, 
     5 => rotation, 
     6 => thickness, 
     7 => ASE, 
     8 => sDA, 
)

## Multi-Objective Optimization Algorithms
### Metaheuristics
pop_size = 20
metaheuristics = ["NSGAII", "OMOPSO"]

### Model-Based (or metamodel)
metamodels_base = ["GPR"]
metamodels_strategies = ["SPEA2"]
metamodels_algorithms = ["$(b)_$(s)" for b in metamodels_base for s in metamodels_strategies]

all_algorithms_phase1 = vcat(metaheuristics, metamodels_algorithms)
n_algorithms_phase1 = length(all_algorithms_phase1)

### Filenames with the results 
filenames_phase1 = ["$(a)_results_0$(r).$(file_extension)" for r in runs for a in all_algorithms_phase1]
filenames_phase1

Pareto Front¶

Layout¶

In [ ]:

layout_weaved = Layout(
    template="plotly_white",
    autosize=false,
    # Define plot size
    width=900, 
    height=540,
    # Legend Position
    # showlegend = False,
    legend=Dict(
        :orientation=>'h',
        :x=>-0.01,
        :y=>-0.2
    ),

    # Define axis
    xaxis=Dict(
        :title=>"sDA",
        :autorange=>true,
        :showgrid=>true,
        :zeroline=>false,
        :showline=>true,
        :ticks=>"",
        :showticklabels=>true,
        :tickformat=>"."
    ),
  
    yaxis=Dict(
        :title=>"ASE",
        :autorange=>true,        
        :showgrid=>true,
        :zeroline=>false,
        :showline=>true,
        :ticks=>"",
        :showticklabels=>true,
        :tickformat=>"."
    )
)

Read Files¶

In [ ]:

# Read algorithms  
dfs1 = load_results(filenames_phase1)
nothing

In [ ]:

dfs1 = [rename!(df, [map(x->x[2], names_mapping) ...]) for df in dfs1]
nothing

In [ ]:

# Compute non_dominated_solutions (per run)
pfs1 = [add_isdominated_cols(df) for df in dfs1]
nothing

In [ ]:

# Computes combined Pareto Front (optimal solutions found from all the algorithms, all the runs)
combined_pf1 = get_combined_PF(dfs1, drop_cols=relevant_cols)
nothing

In [ ]:

#Run this cell only once!!!
pfs1 = [unscale(pf, rotation, -pi, 0.02) for pf in pfs1]
pfs1 = [unscale(pf, thickness, 0, 0.02) for pf in pfs1]
nothing

In [ ]:

first(pfs1[1], 6)

In [ ]:

# Since sDA is actually a maximization, let us use the symmetric operation 
pfs1 = [get_symmetric(pf, sDA) for pf in pfs1]
combined_pf1 = get_symmetric(combined_pf1, sDA)
nothing

In [ ]:

# Sort sDA values in ascending order

## This fixes the error we were getting in the create_pfs_interactive function,
## which would return a different point than the one we selected

pfs1 = [sort(pf, [sDA], rev=false) for pf in pfs1]
nothing

In [ ]:

first(pfs1[1], 6)

Pareto Front Plot¶

In [ ]:

new_backend()

create_pfs(pfs1, x=sDA, y=ASE, tpf=nothing, names=all_algorithms_phase1, 
           colorscale=nothing, colors=["#43a0b5", "#B5557A", "#eb911c"],
           draw_dominated=true, layout=layout_weaved)

LEED V4 Daylight Credit¶

To score in the LEED V4 Daylight Credit a solution must simultaneously meet the following requirements:

$$ ASE < 20\% \\ sDA \geq\ 40\% $$

We selected a few solutions from the Pareto fronts that meet LEED v4 Daylight Credit.

solution	algorithm	m_stripes	rotation	thickness	ASE	sDA
1	NSGAII	7	1.55841	1.5	17.7	59.0
2	OMOPSO	6	1.63841	0.3	11.3	45.0
3	GPR_SPEA2	6	-2.74159	0.9	19.7	45.7