Machine Learning¶

A Summary of lecture "Introduction to Computational Thinking and Data Science", via MITx-6.00.2x (edX)

• toc: true
• badges: true
• comments: true
• author: Chanseok Kang
• categories: [Python, edX, Machine_Learning]
• image: images/ml_block.png

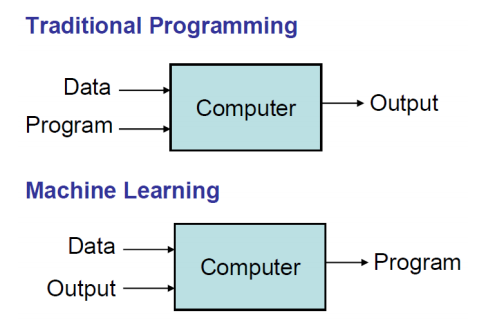
• What is Machine Learning
  • Many useful programs learn something

Note: "Field of study that gives computers the ability to learn without being explicitly programmed" - Arthur Samuel

- Modern statistics meets optimization

• Basic Paradigm
  • Observe set of examples: training data
  • Infer something about process that generated that data
  • Use inference to make predictions about previously unseen data: test data
• All ML Methods Require
  • Representation of the features
  • Distance metric for feature vectors
  • Objective function and constraints
  • Optimization method for learning the model
  • Evaluation method
• Supervised Learning
  • Start with set of feature vector / value pairs
  • Goal : find a model that predicts a value for a previously unseen feature vector
  • Regression models predict a real
    • E.g. linear regression
  • Classification models predict a label (chosen from a finite set of labels)
• Unsupervied Learning
  • Start with a set of feature vectors
  • Goal : uncover some latent structure in the set of feature vectors
  • Clustering the most common technique
    • Define some metric that captures how similar one feature vector is to another
    • Group examples based on this metric
• Choosing Features
  • Features never fully describe the situation
  • Feature Engineering
    • Represent examples by feature vectors that will facilitate generalization
    • Suppose I want to use 100 examples from past to predict which students will pass the final exam
    • Some features surely helpful, e.g., their grade on the midterm, did they do the problem sets, etc.
    • Others might cause me to overfit, e.g., birth month
  • Whant to maximize ratio of useful input to irrelevant input
    • Signal-to-Noise Ratio (SNR)

• K-Nearest Neighbors
  • Distance between vectors
    • Minkowski metric
    $$ dist(X_1, X_2, p) = (\sum_{k=1}^{len}abs({X_1}_k - {X_2}_k)^p)^{\frac{1}{p}} \\ p=1 : \text{Manhattan Distance} \\ p=2 : \text{Euclidean Distance}$$

• Using Distance Matrix for classification
  • Simplest approach is probably nearest neighbor
  • Remember training data
  • When predicting the label of a new example
    • Find the nearest example in the training data
    • Predict the label associated with that example
• Advantage and Disadvantage of KNN
  • Advantages
    • Learning fase, no explicit training
    • No theory required
    • Easy to explain method and results
  • Disadvantages
    • Memory intensive and predictions can take a long time
      • Are better algorithms than brute force
    • No model to shed light on process that generated data

• A more General Approach: Scaling
  • Z-scaling
    • Each feature has a mean of 0 & a standard deviation of 1
  • Interpolation
    • Map minimum value to 0, maximum value to 1, and linearly interpolate

def zScaleFeatures(vals):
    """Assumes vals is a sequence of floats"""
    result = np.array(vals)
    mean = np.mean(vals)
    result = result - mean
    return result/np.std(result)

def iScaleFeatures(vals):
    """Assumes vals is a sequence of floats"""
    minVal, maxVal = min(vals), max(vals)
    fit = np.polyfit([minVal, maxVal], [0, 1], 1)
    return np.polyval(fit, vals)

• Clustering
  • Partition examples into groups (clusters) such that examples in a group are more similar to each other than to examples in other groups
  • Unlike classification, there is not typically a "right answer"
    • Answer dictated by feature vector and distance metric, not by a group truth label
• Optimization Problem

- Why not divide variability by size of cluster?
    - Big and bad worse than small and bad
- Is optimization problem finding a $C$ that minimizes $dissimilarity(C)$?
    - No, otherwise could put each example in its own cluster
- Need constraints, e.g.
    - Minimum distance between clusters
    - Number of clusters

• K-means Clustering
  • Constraint: exactly k non-empty clusters
  • Use a greedy algorithm to find an approximation to minimizing objective function
• Algorithm

randomly chose k examples as initial centroids
while true:
    create k clusters by assigning each example to closest centroid
    compute k new centroids by averaging examples in each cluster
    if centroids don`t change:
        break

• Mitigating Dependence on Initial Centroids

best = kMeans(points)
for t in range(numTrials):
    C = kMeans(points)
    if dissimilarity(C) < dissimilarity(best):
        best = C
return best

• A Pretty Example
  • User k-means to cluster groups of pixels in an image by their color
  • Get the color associated with the centroid of each cluster, i.e., the average color of the cluster
  • For each pixel in the original image, find the centroid that is its nearest neighbor
  • Replaced the pixel by that centroid