Introduction to PyTorch¶
In this first chapter, we introduce basic concepts of neural networks and deep learning using PyTorch library. This is the Summary of lecture "Introduction to Deep Learning with PyTorch", via datacamp.
- toc: true
- badges: true
- comments: true
- author: Chanseok Kang
- categories: [Python, Datacamp, PyTorch, Deep_Learning]
- image: images/graph_exercise.jpg
import torch
import torch.nn as nn
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
Introduction to PyTorch¶
Creating tensors in PyTorch¶
Random tensors are very important in neural networks. Parameters of the neural networks typically are initialized with random weights (random tensors).
Let us start practicing building tensors in PyTorch library. As you know, tensors are arrays with an arbitrary number of dimensions, corresponding to NumPy's ndarrays. You are going to create a random tensor of sizes 3 by 3 and set it to variable your_first_tensor. Then, you will need to print it. Finally, calculate its size in variable tensor_size and print its value.
# Create random Tensor of size 3x3
your_first_tensor = torch.rand(3, 3)
# Calcualtethe shape of the tensor
tensor_size = your_first_tensor.shape
# Print the values of the tensor and its shape
print(your_first_tensor)
print(tensor_size)
tensor([[0.5816, 0.6053, 0.8546],
[0.4350, 0.1575, 0.9543],
[0.8456, 0.5518, 0.9431]])
torch.Size([3, 3])
Matrix multiplication¶
There are many important types of matrices which have their uses in neural networks. Some important matrices are matrices of ones (where each entry is set to 1) and the identity matrix (where the diagonal is set to 1 while all other values are 0). The identity matrix is very important in linear algebra: any matrix multiplied with identity matrix is simply the original matrix.
Let us experiment with these two types of matrices. You are going to build a matrix of ones with shape 3 by 3 called tensor_of_ones and an identity matrix of the same shape, called identity_tensor. We are going to see what happens when we multiply these two matrices, and what happens if we do an element-wise multiplication of them.
# Create a matrix of ones with shape 3x3
tensor_of_ones = torch.ones(3, 3)
# Create a identity matrix with shape 3x3
identity_tensor = torch.eye(3)
# Do a matrix multiplication of tensor_of_ones with identity_tensor
matrices_multiplied = torch.matmul(tensor_of_ones, identity_tensor)
print(matrices_multiplied)
# Do an element-wise multiplication of tensor_of_ones with identity_tensor
element_multipliaction = tensor_of_ones * identity_tensor
print(element_multipliaction)
tensor([[1., 1., 1.],
[1., 1., 1.],
[1., 1., 1.]])
tensor([[1., 0., 0.],
[0., 1., 0.],
[0., 0., 1.]])
matrices_multiplied is same as tensor_of_ones (because identity matrix is the neutral element in matrix multiplication, the product of any matrix multiplied with it gives the original matrix), while element_multiplication is same as identity_tensor.
Forward propagation¶
Forward pass¶
Let's have something resembling more a neural network. The computational graph has been given below. You are going to initialize 3 large random tensors, and then do the operations as given in the computational graph. The final operation is the mean of the tensor, given by torch.mean(your_tensor).
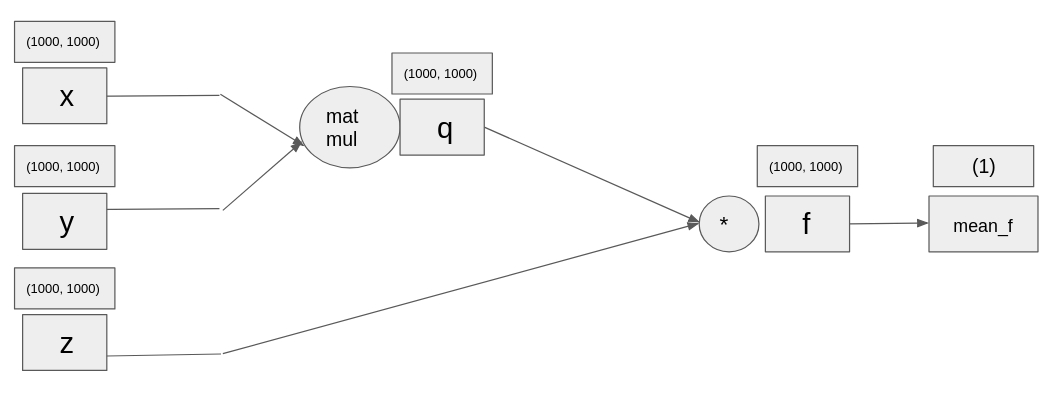
# Intialize tensors x, y, and z
x = torch.rand(1000, 1000)
y = torch.rand(1000, 1000)
z = torch.rand(1000, 1000)
# Multiply x with y
q = torch.matmul(x, y)
# Multiply elementwise z with q
f = z * q
mean_f = torch.mean(f)
print(mean_f)
tensor(124.9414)
Backpropagation by auto-differentiation¶
Backpropagation using PyTorch¶
Here, you are going to use automatic differentiation of PyTorch in order to compute the derivatives of x, y and z from the previous exercise.
# Initialize x, y and z to values 4, -3, and 5
x = torch.tensor(4., requires_grad=True)
y = torch.tensor(-3., requires_grad=True)
z = torch.tensor(5., requires_grad=True)
# Set q to sum of x and y, set f to product of q with z
q = x + y
f = q * z
# Compute the derivative
f.backward()
# Print the gradients
print('Gradient of x is: ' + str(x.grad))
print('Gradient of y is: ' + str(y.grad))
print('Gradient of z is: ' + str(z.grad))
Gradient of x is: tensor(5.) Gradient of y is: tensor(5.) Gradient of z is: tensor(1.)
Calculating gradients in PyTorch¶
Remember the exercise in forward pass? Now that you know how to calculate derivatives, let's make a step forward and start calculating the gradients (derivatives of tensors) of the computational graph you built back then. We have already initialized for you three random tensors of shape (1000, 1000) called x, y and z. First, we multiply tensors x and y, then we do an elementwise multiplication of their product with tensor z, and then we compute its mean. In the end, we compute the derivatives.
The main difference from the previous exercise is the scale of the tensors. While before, tensors x, y and z had just 1 number, now they each have 1 million numbers.
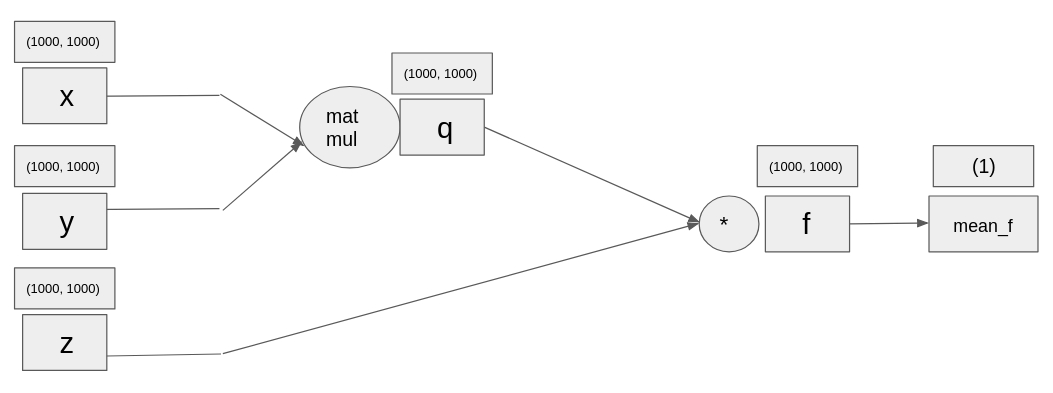
x = torch.rand(1000, 1000, requires_grad=True)
y = torch.rand(1000, 1000, requires_grad=True)
z = torch.rand(1000, 1000, requires_grad=True)
# Multiply tensors x and y
q = torch.matmul(x, y)
# Elementwise multiply tensors z with q
f = z * q
mean_f = torch.mean(f)
# Calculate the gradients
mean_f.backward()
Introduction to Neural Networks¶
Your first neural network¶
You are going to build a neural network in PyTorch, using the hard way. Your input will be images of size (28, 28), so images containing 784 pixels. Your network will contain an input_layer, a hidden layer with 200 units, and an output layer with 10 classes. The input layer has already been created for you. You are going to create the weights, and then do matrix multiplications, getting the results from the network.
input_layer = torch.rand(784)
# Initialize the weights of the neural network
weight_1 = torch.rand(784, 200)
weight_2 = torch.rand(200, 10)
# Multiply input_layer with weight_1
hidden_1 = torch.matmul(input_layer, weight_1)
# Multiply hidden_1 with weight_2
output_layer = torch.matmul(hidden_1, weight_2)
print(output_layer)
tensor([18735.8730, 18511.5098, 20068.1992, 17833.7676, 17848.9141, 18220.7695,
19325.1348, 18821.3984, 19510.9082, 20627.5332])
Your first PyTorch neural network¶
You are going to build the same neural network you built in the previous exercise, but now using the PyTorch way. As a reminder, you have 784 units in the input layer, 200 hidden units and 10 units for the output layer.
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
# Instantiate all 2 linear layers
self.fc1 = nn.Linear(784, 200)
self.fc2 = nn.Linear(200, 10)
def forward(self, x):
# Use the instantiated layers and return x
x = self.fc1(x)
x = self.fc2(x)
return x