Notebook

Several Tips for Improving Neural Network¶

In this post, it will be mentioned about how we can improve the performace of neural network. Especially, we are talking about ReLU activation function, Weight Initialization, Dropout, and Batch Normalization

toc: true
badges: true
comments: true
author: Chanseok Kang
categories: [Python, Deep_Learning, Tensorflow-Keras]
image: images/gradient_descent.gif

In [1]:

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd

plt.rcParams['figure.figsize'] = (16, 10)
plt.rcParams['text.usetex'] = True
plt.rc('font', size=15)

ReLU Activation Function¶

Problem of Sigmoid¶

Previously, we talked about the process happened int neural network. When the input pass througth the network, and generate the output, we called forward propagation. From this, we can measure the error between the predicted output and actual output. Of course, we want to train the neural network for minimizing this error. So we differentiate the the error and update the weight based on this. It is called backpropation.

sigmoid

$$g(z) = \frac{1}{1 + e^{-z}} $$

This is the sigmoid function. We used this for measuring the probability of binary classification. And its range is from 0 to 1. When we apply sigmoid function in the output, sigmoid function will be affected in backpropgation. The problem is that, when we differentiate the middle point of sigmoid function. It doesn't care while we differentiate the sigmoid function in middle point. The problem is when the error goes $\infty$ or $-\infty$. As you can see, when the error is high, the gradient of sigmoid goes to 0, and when the error is negatively high, the gradient of sigmoid goes to 0 too. When we cover the chain rule in previous post, the gradient in post step is used to calculate the overall gradient. So what if error is too high in some nodes, the overall gradient go towards to 0, because of chain rule. This kind of problem is called Vanishing Gradient. Of course, we cannot calculate the gradient, and it is hard to update the weight.

ReLU¶

Here, we introduce the new activation function, Rectified Linear Unit (ReLU for short). Originally, simple linear unit is like this,

$$ f(x) = x $$

But we just consider the range of over 0, and ignore the value less than 0. We can express the form like this,

$$ f(x) = \max(0, x) $$

This form can be explained that, when the input is less than 0, then output will be 0. and input is larger than 0, input will be output itself.

relu

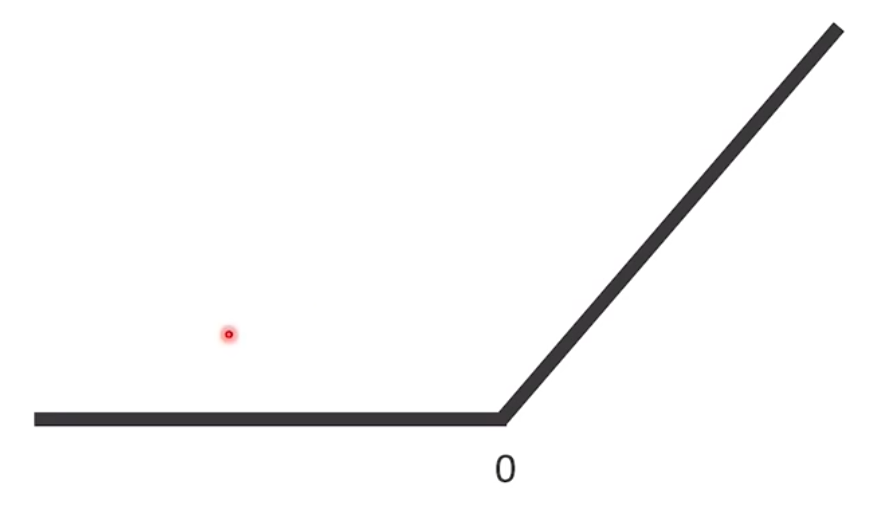
So in this case, how can we analyze its gradient? If the x is larger than 0, its gradient will be 1. Unlike sigmoid, whatever the number of layers is increased, if the error is larger than 0, its gradient maintains and transfers to next step of chain rule. But there is a small problem when the error is less than 0. In this range, its gradient is 0. That is, gradient will be omitted when the error is less than 0. May be this is a same situation in Sigmoid case. But At least, we can main the gradient terms when the error is larger than 0.

There are another variation for handling vanishing gradient problem, such as Exponential Linear Unit (ELU), Scaled Exponential Linear Unit (SELU), Leaky ReLU and so on.

Comparing the performance of each activation function¶

In this example, we will use MNIST dataset for comparing the preformance of each activation function.

In [13]:

from tensorflow.keras.utils import to_categorical
from tensorflow.keras.datasets import mnist

# Load dataset
(X_train, y_train), (X_test, y_test) = mnist.load_data()
print(X_train.shape, X_test.shape)

# Expand the dimension from 2D to 3D
X_train = tf.expand_dims(X_train, axis=-1)
X_test = tf.expand_dims(X_test, axis=-1)
print(X_train.shape, X_test.shape)

(60000, 28, 28) (10000, 28, 28)
(60000, 28, 28, 1) (10000, 28, 28, 1)

Maybe someone will be confused in expanding the dimension. That's because tensorflow enforce image inputs shapes like [batch_size, height, width, channel]. But MNIST dataset included in keras, doesn't have information of channel. So we expand the dimension in the end of dataset for expressing its channel(you know that the channel in MNIST is grayscale, so it is 0)

And its image is grayscale, so the range of data is from 0 to 255. And it is helpful for training while its dataset is normalized. So we apply the normalization.

In [14]:

X_train = tf.cast(X_train, tf.float32) / 255.0
X_test = tf.cast(X_test, tf.float32) / 255.0

And the range of label is from 0 to 9. And its type is categorical. So we need to convert the label with one-hot encoding. Keras offers to_categorical APIs to do this. (There are so many approaches for one-hot encoding, we can try it by your mind).

In [15]:

y_train = to_categorical(y_train, num_classes=10)
y_test = to_categorical(y_test, num_classes=10)

At last, we are going to implement network. In this case, we will build it with class object. Note that, to implement model with class object, we need to delegate the tf.keras.Model as an parent class.

Note: We add the training argument while implementing call function. Its purpose is to separate the feature between training and test(or inference). It`ll be used in Dropout section, later in the post.

In [16]:

class Model(tf.keras.Model):
    def __init__(self, label_dim):
        super(Model, self).__init__()
        
        # Weight initialization (Normal Initializer)
        weight_init = tf.keras.initializers.RandomNormal()
        
        # Sequential Model 
        self.model = tf.keras.Sequential()
        self.model.add(tf.keras.layers.Flatten()) # [N, 28, 28, 1] -> [N, 784]
        for _ in range(2):
            # [N, 784] -> [N, 256] -> [N, 256]
            self.model.add(tf.keras.layers.Dense(256, use_bias=True, kernel_initializer=weight_init))
            self.model.add(tf.keras.layers.Activation(tf.keras.activations.relu))
        self.model.add(tf.keras.layers.Dense(label_dim, use_bias=True, kernel_initializer=weight_init))
        
    def call(self, x, training=None, mask=None):
        x = self.model(x)
        return x

Next, we need to define loss function. Here, we will use softmax cross entropy loss since ourl task is multi label classficiation. Of course, tensorflow offers simple API to calculate it easily. Just calculate the logits (the output generated from your model) and labels, and input it.

In [17]:

# Loss function: Softmax Cross Entropy
def loss_fn(model, images, labels):
    logits = model(images, training=True)
    loss = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=logits, labels=labels))
    return loss

# Accuracy function for inference
def accuracy_fn(model, images, labels):
    logits = model(images, training=False)
    predict = tf.equal(tf.argmax(logits, -1), tf.argmax(labels, -1))
    accuracy = tf.reduce_mean(tf.cast(predict, tf.float32))
    return accuracy

# Gradient function
def grad(model, images, labels):
    with tf.GradientTape() as tape:
        loss = loss_fn(model, images, labels)
    return tape.gradient(loss, model.variables)

Then, we can set model hyperparameters such as learning rate, epochs, batch sizes and so on.

In [18]:

# Parameters
learning_rate = 0.001
batch_size = 128

training_epochs = 1
training_iter = len(X_train) // batch_size

label_dim=10

optimizer = tf.keras.optimizers.Adam(learning_rate=learning_rate)

We can make graph input from original dataset. We already saw this in previous examples. Since, the memory usage is very large if we load whole dataset into memory, we sliced each dataset with batch size.

In [19]:

# Graph input using Dataset API
train_ds = tf.data.Dataset.from_tensor_slices((X_train, y_train)).\
           shuffle(buffer_size=100000).\
           prefetch(buffer_size=batch_size).\
           batch(batch_size)

test_ds = tf.data.Dataset.from_tensor_slices((X_test, y_test)).\
          prefetch(buffer_size=len(X_test)).\
          batch(len(X_test))

In the training step, we instantiate the model and set the checkpoint. Checkpoint is the model save feature during training. So when the model training is failed due to the unexpected external problem, if we set the checkpoint, then we can reload the model at the beginning of last failure point.

In [20]:

import os
from time import time

def load(model, checkpoint_dir):
    print(" [*] Reading checkpoints...")

    ckpt = tf.train.get_checkpoint_state(checkpoint_dir)
    if ckpt :
        ckpt_name = os.path.basename(ckpt.model_checkpoint_path)
        checkpoint = tf.train.Checkpoint(dnn=model)
        checkpoint.restore(save_path=os.path.join(checkpoint_dir, ckpt_name))
        counter = int(ckpt_name.split('-')[1])
        print(" [*] Success to read {}".format(ckpt_name))
        return True, counter
    else:
        print(" [*] Failed to find a checkpoint")
        return False, 0

def check_folder(dir):
    if not os.path.exists(dir):
        os.makedirs(dir)
    return dir

""" Writer """
checkpoint_dir = 'checkpoints'
logs_dir = 'logs'

model_dir = 'nn_softmax'

checkpoint_dir = os.path.join(checkpoint_dir, model_dir)
check_folder(checkpoint_dir)
checkpoint_prefix = os.path.join(checkpoint_dir, model_dir)
logs_dir = os.path.join(logs_dir, model_dir)

In [21]:

model = Model(label_dim)
start_time =time()

# Set checkpoint
checkpoint = tf.train.Checkpoint(dnn=model)

# Restore checkpoint if it exists
could_load, checkpoint_counter = load(model, checkpoint_dir)

if could_load:
    start_epoch = (int)(checkpoint_counter / training_iter)        
    counter = checkpoint_counter        
    print(" [*] Load SUCCESS")
else:
    start_epoch = 0
    start_iteration = 0
    counter = 0
    print(" [!] Load failed...")
    
# train phase
for epoch in range(start_epoch, training_epochs):
    for idx, (train_input, train_label) in enumerate(train_ds):            
        grads = grad(model, train_input, train_label)
        optimizer.apply_gradients(grads_and_vars=zip(grads, model.variables))

        train_loss = loss_fn(model, train_input, train_label)
        train_accuracy = accuracy_fn(model, train_input, train_label)
                
        for test_input, test_label in test_ds:                
            test_accuracy = accuracy_fn(model, test_input, test_label)

        print(
            "Epoch: [%2d] [%5d/%5d] time: %4.4f, train_loss: %.8f, train_accuracy: %.4f, test_Accuracy: %.4f" \
            % (epoch, idx, training_iter, time() - start_time, train_loss, train_accuracy,
           test_accuracy))
        counter += 1                
checkpoint.save(file_prefix=checkpoint_prefix + '-{}'.format(counter))

 [*] Reading checkpoints...
 [*] Failed to find a checkpoint
 [!] Load failed...
Epoch: [ 0] [    0/  468] time: 0.2491, train_loss: 2.15030980, train_accuracy: 0.2266, test_Accuracy: 0.1452
Epoch: [ 0] [    1/  468] time: 0.3121, train_loss: 2.15283918, train_accuracy: 0.1953, test_Accuracy: 0.2136
Epoch: [ 0] [    2/  468] time: 0.3721, train_loss: 2.07774782, train_accuracy: 0.4297, test_Accuracy: 0.3395
Epoch: [ 0] [    3/  468] time: 0.4331, train_loss: 1.97704232, train_accuracy: 0.4609, test_Accuracy: 0.4211
Epoch: [ 0] [    4/  468] time: 0.4951, train_loss: 1.93319905, train_accuracy: 0.5078, test_Accuracy: 0.4982
Epoch: [ 0] [    5/  468] time: 0.5631, train_loss: 1.84458375, train_accuracy: 0.6172, test_Accuracy: 0.6005
Epoch: [ 0] [    6/  468] time: 0.6231, train_loss: 1.71073520, train_accuracy: 0.6875, test_Accuracy: 0.6867
Epoch: [ 0] [    7/  468] time: 0.6842, train_loss: 1.68754315, train_accuracy: 0.6719, test_Accuracy: 0.7173
Epoch: [ 0] [    8/  468] time: 0.7452, train_loss: 1.56382334, train_accuracy: 0.7188, test_Accuracy: 0.7309
Epoch: [ 0] [    9/  468] time: 0.8052, train_loss: 1.37600899, train_accuracy: 0.8203, test_Accuracy: 0.7405
Epoch: [ 0] [   10/  468] time: 0.8662, train_loss: 1.38046825, train_accuracy: 0.7422, test_Accuracy: 0.7595
Epoch: [ 0] [   11/  468] time: 0.9272, train_loss: 1.20876694, train_accuracy: 0.7812, test_Accuracy: 0.7675
Epoch: [ 0] [   12/  468] time: 0.9873, train_loss: 1.14961326, train_accuracy: 0.7500, test_Accuracy: 0.7821
Epoch: [ 0] [   13/  468] time: 1.0492, train_loss: 0.97968102, train_accuracy: 0.8047, test_Accuracy: 0.7916
Epoch: [ 0] [   14/  468] time: 1.1092, train_loss: 0.86035222, train_accuracy: 0.8359, test_Accuracy: 0.8006
Epoch: [ 0] [   15/  468] time: 1.1713, train_loss: 0.93435884, train_accuracy: 0.7578, test_Accuracy: 0.8078
Epoch: [ 0] [   16/  468] time: 1.2353, train_loss: 0.77967739, train_accuracy: 0.8203, test_Accuracy: 0.8119
Epoch: [ 0] [   17/  468] time: 1.2973, train_loss: 0.82329828, train_accuracy: 0.7969, test_Accuracy: 0.8164
Epoch: [ 0] [   18/  468] time: 1.3593, train_loss: 0.76127410, train_accuracy: 0.7969, test_Accuracy: 0.8252
Epoch: [ 0] [   19/  468] time: 1.4233, train_loss: 0.59374988, train_accuracy: 0.8828, test_Accuracy: 0.8308
Epoch: [ 0] [   20/  468] time: 1.4853, train_loss: 0.65207708, train_accuracy: 0.8359, test_Accuracy: 0.8344
Epoch: [ 0] [   21/  468] time: 1.5493, train_loss: 0.52844054, train_accuracy: 0.8750, test_Accuracy: 0.8334
Epoch: [ 0] [   22/  468] time: 1.6114, train_loss: 0.58252573, train_accuracy: 0.8359, test_Accuracy: 0.8299
Epoch: [ 0] [   23/  468] time: 1.6744, train_loss: 0.60676157, train_accuracy: 0.8438, test_Accuracy: 0.8308
Epoch: [ 0] [   24/  468] time: 1.7354, train_loss: 0.52588582, train_accuracy: 0.8828, test_Accuracy: 0.8374
Epoch: [ 0] [   25/  468] time: 1.7974, train_loss: 0.49769706, train_accuracy: 0.8672, test_Accuracy: 0.8474
Epoch: [ 0] [   26/  468] time: 1.8594, train_loss: 0.50299680, train_accuracy: 0.8906, test_Accuracy: 0.8379
Epoch: [ 0] [   27/  468] time: 1.9214, train_loss: 0.46636519, train_accuracy: 0.8594, test_Accuracy: 0.8283
Epoch: [ 0] [   28/  468] time: 1.9834, train_loss: 0.59428501, train_accuracy: 0.8281, test_Accuracy: 0.8398
Epoch: [ 0] [   29/  468] time: 2.0455, train_loss: 0.56251818, train_accuracy: 0.8047, test_Accuracy: 0.8509
Epoch: [ 0] [   30/  468] time: 2.1065, train_loss: 0.43280989, train_accuracy: 0.8672, test_Accuracy: 0.8555
Epoch: [ 0] [   31/  468] time: 2.1685, train_loss: 0.35328683, train_accuracy: 0.9062, test_Accuracy: 0.8549
Epoch: [ 0] [   32/  468] time: 2.2315, train_loss: 0.40768445, train_accuracy: 0.8594, test_Accuracy: 0.8494
Epoch: [ 0] [   33/  468] time: 2.2935, train_loss: 0.54843789, train_accuracy: 0.8125, test_Accuracy: 0.8529
Epoch: [ 0] [   34/  468] time: 2.3555, train_loss: 0.53448266, train_accuracy: 0.8281, test_Accuracy: 0.8615
Epoch: [ 0] [   35/  468] time: 2.4185, train_loss: 0.48472366, train_accuracy: 0.8594, test_Accuracy: 0.8612
Epoch: [ 0] [   36/  468] time: 2.4806, train_loss: 0.50503701, train_accuracy: 0.8594, test_Accuracy: 0.8586
Epoch: [ 0] [   37/  468] time: 2.5446, train_loss: 0.28531340, train_accuracy: 0.9297, test_Accuracy: 0.8637
Epoch: [ 0] [   38/  468] time: 2.6066, train_loss: 0.42061746, train_accuracy: 0.8594, test_Accuracy: 0.8762
Epoch: [ 0] [   39/  468] time: 2.6686, train_loss: 0.43485492, train_accuracy: 0.8750, test_Accuracy: 0.8860
Epoch: [ 0] [   40/  468] time: 2.7326, train_loss: 0.41276726, train_accuracy: 0.9062, test_Accuracy: 0.8844
Epoch: [ 0] [   41/  468] time: 2.7946, train_loss: 0.28081536, train_accuracy: 0.9062, test_Accuracy: 0.8801
Epoch: [ 0] [   42/  468] time: 2.8576, train_loss: 0.35974616, train_accuracy: 0.9141, test_Accuracy: 0.8688
Epoch: [ 0] [   43/  468] time: 2.9207, train_loss: 0.42074358, train_accuracy: 0.8594, test_Accuracy: 0.8673
Epoch: [ 0] [   44/  468] time: 2.9837, train_loss: 0.32754454, train_accuracy: 0.8828, test_Accuracy: 0.8779
Epoch: [ 0] [   45/  468] time: 3.0457, train_loss: 0.32231712, train_accuracy: 0.8828, test_Accuracy: 0.8874
Epoch: [ 0] [   46/  468] time: 3.1087, train_loss: 0.36304191, train_accuracy: 0.8984, test_Accuracy: 0.8924
Epoch: [ 0] [   47/  468] time: 3.1697, train_loss: 0.32422566, train_accuracy: 0.9141, test_Accuracy: 0.8952
Epoch: [ 0] [   48/  468] time: 3.2327, train_loss: 0.38969386, train_accuracy: 0.8906, test_Accuracy: 0.8958
Epoch: [ 0] [   49/  468] time: 3.2957, train_loss: 0.43795654, train_accuracy: 0.8672, test_Accuracy: 0.8888
Epoch: [ 0] [   50/  468] time: 3.3598, train_loss: 0.43280196, train_accuracy: 0.8906, test_Accuracy: 0.8884
Epoch: [ 0] [   51/  468] time: 3.4228, train_loss: 0.40492800, train_accuracy: 0.8750, test_Accuracy: 0.8937
Epoch: [ 0] [   52/  468] time: 3.4858, train_loss: 0.45982653, train_accuracy: 0.8594, test_Accuracy: 0.8952
Epoch: [ 0] [   53/  468] time: 3.5468, train_loss: 0.32028058, train_accuracy: 0.8828, test_Accuracy: 0.8982
Epoch: [ 0] [   54/  468] time: 3.6078, train_loss: 0.31702724, train_accuracy: 0.8906, test_Accuracy: 0.8973
Epoch: [ 0] [   55/  468] time: 3.6708, train_loss: 0.41682231, train_accuracy: 0.8906, test_Accuracy: 0.8983
Epoch: [ 0] [   56/  468] time: 3.7339, train_loss: 0.21412303, train_accuracy: 0.9453, test_Accuracy: 0.8946
Epoch: [ 0] [   57/  468] time: 3.7969, train_loss: 0.46382612, train_accuracy: 0.8828, test_Accuracy: 0.8953
Epoch: [ 0] [   58/  468] time: 3.8609, train_loss: 0.27687752, train_accuracy: 0.8984, test_Accuracy: 0.8997
Epoch: [ 0] [   59/  468] time: 3.9239, train_loss: 0.27421039, train_accuracy: 0.9609, test_Accuracy: 0.9016
Epoch: [ 0] [   60/  468] time: 3.9869, train_loss: 0.37226164, train_accuracy: 0.8672, test_Accuracy: 0.8985
Epoch: [ 0] [   61/  468] time: 4.0499, train_loss: 0.29157472, train_accuracy: 0.9062, test_Accuracy: 0.8959
Epoch: [ 0] [   62/  468] time: 4.1129, train_loss: 0.26518056, train_accuracy: 0.9141, test_Accuracy: 0.8958
Epoch: [ 0] [   63/  468] time: 4.1780, train_loss: 0.49583787, train_accuracy: 0.8906, test_Accuracy: 0.8961
Epoch: [ 0] [   64/  468] time: 4.2420, train_loss: 0.26262233, train_accuracy: 0.9453, test_Accuracy: 0.9020
Epoch: [ 0] [   65/  468] time: 4.3060, train_loss: 0.38248271, train_accuracy: 0.8906, test_Accuracy: 0.9087
Epoch: [ 0] [   66/  468] time: 4.3691, train_loss: 0.25547937, train_accuracy: 0.8984, test_Accuracy: 0.9130
Epoch: [ 0] [   67/  468] time: 4.4331, train_loss: 0.37517202, train_accuracy: 0.9062, test_Accuracy: 0.9101
Epoch: [ 0] [   68/  468] time: 4.4951, train_loss: 0.24114588, train_accuracy: 0.9453, test_Accuracy: 0.9071
Epoch: [ 0] [   69/  468] time: 4.5591, train_loss: 0.30137047, train_accuracy: 0.9297, test_Accuracy: 0.9033
Epoch: [ 0] [   70/  468] time: 4.6231, train_loss: 0.35740495, train_accuracy: 0.9297, test_Accuracy: 0.9020
Epoch: [ 0] [   71/  468] time: 4.6841, train_loss: 0.41990116, train_accuracy: 0.8750, test_Accuracy: 0.9031
Epoch: [ 0] [   72/  468] time: 4.7461, train_loss: 0.32718772, train_accuracy: 0.9062, test_Accuracy: 0.9058
Epoch: [ 0] [   73/  468] time: 4.8092, train_loss: 0.32029492, train_accuracy: 0.9141, test_Accuracy: 0.9101
Epoch: [ 0] [   74/  468] time: 4.8702, train_loss: 0.34653026, train_accuracy: 0.8906, test_Accuracy: 0.9116
Epoch: [ 0] [   75/  468] time: 4.9342, train_loss: 0.24824965, train_accuracy: 0.9219, test_Accuracy: 0.9108
Epoch: [ 0] [   76/  468] time: 4.9972, train_loss: 0.39011461, train_accuracy: 0.9062, test_Accuracy: 0.9096
Epoch: [ 0] [   77/  468] time: 5.0612, train_loss: 0.36081627, train_accuracy: 0.9062, test_Accuracy: 0.9024
Epoch: [ 0] [   78/  468] time: 5.1252, train_loss: 0.32710829, train_accuracy: 0.8906, test_Accuracy: 0.9033
Epoch: [ 0] [   79/  468] time: 5.1892, train_loss: 0.30211586, train_accuracy: 0.9297, test_Accuracy: 0.9091
Epoch: [ 0] [   80/  468] time: 5.2543, train_loss: 0.26078090, train_accuracy: 0.9141, test_Accuracy: 0.9107
Epoch: [ 0] [   81/  468] time: 5.3173, train_loss: 0.30378014, train_accuracy: 0.8984, test_Accuracy: 0.9113
Epoch: [ 0] [   82/  468] time: 5.3803, train_loss: 0.36620122, train_accuracy: 0.8984, test_Accuracy: 0.9108
Epoch: [ 0] [   83/  468] time: 5.4433, train_loss: 0.32149518, train_accuracy: 0.9062, test_Accuracy: 0.9101
Epoch: [ 0] [   84/  468] time: 5.5093, train_loss: 0.29505837, train_accuracy: 0.9375, test_Accuracy: 0.9065
Epoch: [ 0] [   85/  468] time: 5.5703, train_loss: 0.33091930, train_accuracy: 0.8906, test_Accuracy: 0.9053
Epoch: [ 0] [   86/  468] time: 5.6333, train_loss: 0.38630185, train_accuracy: 0.9141, test_Accuracy: 0.9068
Epoch: [ 0] [   87/  468] time: 5.6984, train_loss: 0.41085005, train_accuracy: 0.8984, test_Accuracy: 0.9038
Epoch: [ 0] [   88/  468] time: 5.7624, train_loss: 0.31273714, train_accuracy: 0.8984, test_Accuracy: 0.9055
Epoch: [ 0] [   89/  468] time: 5.8244, train_loss: 0.29829884, train_accuracy: 0.9062, test_Accuracy: 0.9007
Epoch: [ 0] [   90/  468] time: 5.8884, train_loss: 0.42691422, train_accuracy: 0.8750, test_Accuracy: 0.9044
Epoch: [ 0] [   91/  468] time: 5.9544, train_loss: 0.19773099, train_accuracy: 0.9609, test_Accuracy: 0.9092
Epoch: [ 0] [   92/  468] time: 6.0164, train_loss: 0.33233923, train_accuracy: 0.9062, test_Accuracy: 0.9121
Epoch: [ 0] [   93/  468] time: 6.0804, train_loss: 0.29973486, train_accuracy: 0.8906, test_Accuracy: 0.9118
Epoch: [ 0] [   94/  468] time: 6.1455, train_loss: 0.35997713, train_accuracy: 0.8594, test_Accuracy: 0.9134
Epoch: [ 0] [   95/  468] time: 6.2085, train_loss: 0.26744440, train_accuracy: 0.9297, test_Accuracy: 0.9142
Epoch: [ 0] [   96/  468] time: 6.2715, train_loss: 0.30835310, train_accuracy: 0.8828, test_Accuracy: 0.9148
Epoch: [ 0] [   97/  468] time: 6.3365, train_loss: 0.41458651, train_accuracy: 0.9062, test_Accuracy: 0.9150
Epoch: [ 0] [   98/  468] time: 6.3995, train_loss: 0.25687534, train_accuracy: 0.9453, test_Accuracy: 0.9163
Epoch: [ 0] [   99/  468] time: 6.4635, train_loss: 0.35696569, train_accuracy: 0.9062, test_Accuracy: 0.9199
Epoch: [ 0] [  100/  468] time: 6.5275, train_loss: 0.31090885, train_accuracy: 0.9141, test_Accuracy: 0.9179
Epoch: [ 0] [  101/  468] time: 6.5906, train_loss: 0.26249218, train_accuracy: 0.9297, test_Accuracy: 0.9162
Epoch: [ 0] [  102/  468] time: 6.6561, train_loss: 0.21557218, train_accuracy: 0.9297, test_Accuracy: 0.9161
Epoch: [ 0] [  103/  468] time: 6.7241, train_loss: 0.26813257, train_accuracy: 0.9297, test_Accuracy: 0.9177
Epoch: [ 0] [  104/  468] time: 6.7921, train_loss: 0.26840457, train_accuracy: 0.9297, test_Accuracy: 0.9204
Epoch: [ 0] [  105/  468] time: 6.8581, train_loss: 0.41396719, train_accuracy: 0.8906, test_Accuracy: 0.9244
Epoch: [ 0] [  106/  468] time: 6.9231, train_loss: 0.20383561, train_accuracy: 0.9297, test_Accuracy: 0.9254
Epoch: [ 0] [  107/  468] time: 6.9891, train_loss: 0.19787546, train_accuracy: 0.9531, test_Accuracy: 0.9237
Epoch: [ 0] [  108/  468] time: 7.0551, train_loss: 0.34419316, train_accuracy: 0.8828, test_Accuracy: 0.9234
Epoch: [ 0] [  109/  468] time: 7.1212, train_loss: 0.25148118, train_accuracy: 0.9062, test_Accuracy: 0.9208
Epoch: [ 0] [  110/  468] time: 7.1912, train_loss: 0.27769178, train_accuracy: 0.9219, test_Accuracy: 0.9171
Epoch: [ 0] [  111/  468] time: 7.2572, train_loss: 0.28824270, train_accuracy: 0.9375, test_Accuracy: 0.9185
Epoch: [ 0] [  112/  468] time: 7.3232, train_loss: 0.31092465, train_accuracy: 0.9219, test_Accuracy: 0.9225
Epoch: [ 0] [  113/  468] time: 7.3892, train_loss: 0.29452521, train_accuracy: 0.9219, test_Accuracy: 0.9233
Epoch: [ 0] [  114/  468] time: 7.4562, train_loss: 0.27070722, train_accuracy: 0.9297, test_Accuracy: 0.9252
Epoch: [ 0] [  115/  468] time: 7.5223, train_loss: 0.32723838, train_accuracy: 0.9297, test_Accuracy: 0.9234
Epoch: [ 0] [  116/  468] time: 7.5863, train_loss: 0.20157896, train_accuracy: 0.9453, test_Accuracy: 0.9200
Epoch: [ 0] [  117/  468] time: 7.6533, train_loss: 0.22456610, train_accuracy: 0.9609, test_Accuracy: 0.9177
Epoch: [ 0] [  118/  468] time: 7.7173, train_loss: 0.22926557, train_accuracy: 0.8984, test_Accuracy: 0.9195
Epoch: [ 0] [  119/  468] time: 7.7813, train_loss: 0.25986317, train_accuracy: 0.9219, test_Accuracy: 0.9240
Epoch: [ 0] [  120/  468] time: 7.8463, train_loss: 0.33479416, train_accuracy: 0.9297, test_Accuracy: 0.9245
Epoch: [ 0] [  121/  468] time: 7.9123, train_loss: 0.20577163, train_accuracy: 0.9297, test_Accuracy: 0.9252
Epoch: [ 0] [  122/  468] time: 7.9774, train_loss: 0.28843778, train_accuracy: 0.9062, test_Accuracy: 0.9246
Epoch: [ 0] [  123/  468] time: 8.0434, train_loss: 0.23792754, train_accuracy: 0.9375, test_Accuracy: 0.9240
Epoch: [ 0] [  124/  468] time: 8.1084, train_loss: 0.23528665, train_accuracy: 0.9141, test_Accuracy: 0.9243
Epoch: [ 0] [  125/  468] time: 8.1724, train_loss: 0.31796750, train_accuracy: 0.8984, test_Accuracy: 0.9254
Epoch: [ 0] [  126/  468] time: 8.2354, train_loss: 0.19401328, train_accuracy: 0.9219, test_Accuracy: 0.9265
Epoch: [ 0] [  127/  468] time: 8.3004, train_loss: 0.16888312, train_accuracy: 0.9453, test_Accuracy: 0.9243
Epoch: [ 0] [  128/  468] time: 8.3644, train_loss: 0.32847032, train_accuracy: 0.8984, test_Accuracy: 0.9222
Epoch: [ 0] [  129/  468] time: 8.4295, train_loss: 0.27693975, train_accuracy: 0.8906, test_Accuracy: 0.9219
Epoch: [ 0] [  130/  468] time: 8.4945, train_loss: 0.22807607, train_accuracy: 0.9375, test_Accuracy: 0.9209
Epoch: [ 0] [  131/  468] time: 8.5595, train_loss: 0.22568117, train_accuracy: 0.9375, test_Accuracy: 0.9244
Epoch: [ 0] [  132/  468] time: 8.6225, train_loss: 0.27173108, train_accuracy: 0.9062, test_Accuracy: 0.9284
Epoch: [ 0] [  133/  468] time: 8.6865, train_loss: 0.35024145, train_accuracy: 0.8906, test_Accuracy: 0.9275
Epoch: [ 0] [  134/  468] time: 8.7495, train_loss: 0.38954973, train_accuracy: 0.8984, test_Accuracy: 0.9271
Epoch: [ 0] [  135/  468] time: 8.8135, train_loss: 0.21493477, train_accuracy: 0.9453, test_Accuracy: 0.9241
Epoch: [ 0] [  136/  468] time: 8.8786, train_loss: 0.25806636, train_accuracy: 0.9297, test_Accuracy: 0.9189
Epoch: [ 0] [  137/  468] time: 8.9446, train_loss: 0.20212270, train_accuracy: 0.9219, test_Accuracy: 0.9154
Epoch: [ 0] [  138/  468] time: 9.0096, train_loss: 0.28960535, train_accuracy: 0.9297, test_Accuracy: 0.9127
Epoch: [ 0] [  139/  468] time: 9.0726, train_loss: 0.35245126, train_accuracy: 0.9297, test_Accuracy: 0.9151
Epoch: [ 0] [  140/  468] time: 9.1386, train_loss: 0.26913369, train_accuracy: 0.9219, test_Accuracy: 0.9212
Epoch: [ 0] [  141/  468] time: 9.2026, train_loss: 0.27163938, train_accuracy: 0.9141, test_Accuracy: 0.9264
Epoch: [ 0] [  142/  468] time: 9.2716, train_loss: 0.22377852, train_accuracy: 0.9453, test_Accuracy: 0.9282
Epoch: [ 0] [  143/  468] time: 9.3377, train_loss: 0.27024600, train_accuracy: 0.9297, test_Accuracy: 0.9295
Epoch: [ 0] [  144/  468] time: 9.4077, train_loss: 0.29181483, train_accuracy: 0.9219, test_Accuracy: 0.9280
Epoch: [ 0] [  145/  468] time: 9.4727, train_loss: 0.36190426, train_accuracy: 0.8906, test_Accuracy: 0.9266
Epoch: [ 0] [  146/  468] time: 9.5367, train_loss: 0.24922608, train_accuracy: 0.9531, test_Accuracy: 0.9274
Epoch: [ 0] [  147/  468] time: 9.6007, train_loss: 0.32412627, train_accuracy: 0.8906, test_Accuracy: 0.9272
Epoch: [ 0] [  148/  468] time: 9.6667, train_loss: 0.30410588, train_accuracy: 0.9375, test_Accuracy: 0.9282
Epoch: [ 0] [  149/  468] time: 9.7358, train_loss: 0.26427433, train_accuracy: 0.9297, test_Accuracy: 0.9270
Epoch: [ 0] [  150/  468] time: 9.7998, train_loss: 0.30568987, train_accuracy: 0.8828, test_Accuracy: 0.9293
Epoch: [ 0] [  151/  468] time: 9.8678, train_loss: 0.26532823, train_accuracy: 0.9219, test_Accuracy: 0.9342
Epoch: [ 0] [  152/  468] time: 9.9348, train_loss: 0.29068148, train_accuracy: 0.9141, test_Accuracy: 0.9331
Epoch: [ 0] [  153/  468] time: 10.0028, train_loss: 0.23632655, train_accuracy: 0.9062, test_Accuracy: 0.9335
Epoch: [ 0] [  154/  468] time: 10.0688, train_loss: 0.25320745, train_accuracy: 0.9141, test_Accuracy: 0.9335
Epoch: [ 0] [  155/  468] time: 10.1358, train_loss: 0.22654940, train_accuracy: 0.9297, test_Accuracy: 0.9322
Epoch: [ 0] [  156/  468] time: 10.2039, train_loss: 0.23808193, train_accuracy: 0.9531, test_Accuracy: 0.9322
Epoch: [ 0] [  157/  468] time: 10.2719, train_loss: 0.24162428, train_accuracy: 0.9219, test_Accuracy: 0.9319
Epoch: [ 0] [  158/  468] time: 10.3429, train_loss: 0.23989542, train_accuracy: 0.9219, test_Accuracy: 0.9321
Epoch: [ 0] [  159/  468] time: 10.4099, train_loss: 0.20225845, train_accuracy: 0.9609, test_Accuracy: 0.9344
Epoch: [ 0] [  160/  468] time: 10.4769, train_loss: 0.23110092, train_accuracy: 0.9219, test_Accuracy: 0.9349
Epoch: [ 0] [  161/  468] time: 10.5449, train_loss: 0.21751849, train_accuracy: 0.9375, test_Accuracy: 0.9339
Epoch: [ 0] [  162/  468] time: 10.6090, train_loss: 0.16106503, train_accuracy: 0.9375, test_Accuracy: 0.9329
Epoch: [ 0] [  163/  468] time: 10.6740, train_loss: 0.20251328, train_accuracy: 0.9219, test_Accuracy: 0.9310
Epoch: [ 0] [  164/  468] time: 10.7390, train_loss: 0.23731238, train_accuracy: 0.9062, test_Accuracy: 0.9310
Epoch: [ 0] [  165/  468] time: 10.8030, train_loss: 0.22041874, train_accuracy: 0.9297, test_Accuracy: 0.9310
Epoch: [ 0] [  166/  468] time: 10.8670, train_loss: 0.27926773, train_accuracy: 0.9219, test_Accuracy: 0.9344
Epoch: [ 0] [  167/  468] time: 10.9310, train_loss: 0.20776446, train_accuracy: 0.9453, test_Accuracy: 0.9344
Epoch: [ 0] [  168/  468] time: 10.9940, train_loss: 0.16684905, train_accuracy: 0.9609, test_Accuracy: 0.9354
Epoch: [ 0] [  169/  468] time: 11.0601, train_loss: 0.17609364, train_accuracy: 0.9453, test_Accuracy: 0.9369
Epoch: [ 0] [  170/  468] time: 11.1241, train_loss: 0.23581663, train_accuracy: 0.9219, test_Accuracy: 0.9365
Epoch: [ 0] [  171/  468] time: 11.1891, train_loss: 0.15646684, train_accuracy: 0.9688, test_Accuracy: 0.9345
Epoch: [ 0] [  172/  468] time: 11.2541, train_loss: 0.31185722, train_accuracy: 0.9219, test_Accuracy: 0.9351
Epoch: [ 0] [  173/  468] time: 11.3191, train_loss: 0.22194964, train_accuracy: 0.9297, test_Accuracy: 0.9371
Epoch: [ 0] [  174/  468] time: 11.3821, train_loss: 0.17540474, train_accuracy: 0.9531, test_Accuracy: 0.9374
Epoch: [ 0] [  175/  468] time: 11.4471, train_loss: 0.30563429, train_accuracy: 0.8906, test_Accuracy: 0.9379
Epoch: [ 0] [  176/  468] time: 11.5142, train_loss: 0.18680054, train_accuracy: 0.9609, test_Accuracy: 0.9371
Epoch: [ 0] [  177/  468] time: 11.5782, train_loss: 0.18710050, train_accuracy: 0.9453, test_Accuracy: 0.9376
Epoch: [ 0] [  178/  468] time: 11.6412, train_loss: 0.14796190, train_accuracy: 0.9609, test_Accuracy: 0.9345
Epoch: [ 0] [  179/  468] time: 11.7042, train_loss: 0.21705720, train_accuracy: 0.9375, test_Accuracy: 0.9326
Epoch: [ 0] [  180/  468] time: 11.7682, train_loss: 0.20004642, train_accuracy: 0.9531, test_Accuracy: 0.9308
Epoch: [ 0] [  181/  468] time: 11.8292, train_loss: 0.18277654, train_accuracy: 0.9375, test_Accuracy: 0.9317
Epoch: [ 0] [  182/  468] time: 11.8932, train_loss: 0.23364887, train_accuracy: 0.9219, test_Accuracy: 0.9354
Epoch: [ 0] [  183/  468] time: 11.9563, train_loss: 0.18390165, train_accuracy: 0.9375, test_Accuracy: 0.9385
Epoch: [ 0] [  184/  468] time: 12.0203, train_loss: 0.18731409, train_accuracy: 0.9609, test_Accuracy: 0.9387
Epoch: [ 0] [  185/  468] time: 12.0833, train_loss: 0.13293701, train_accuracy: 0.9688, test_Accuracy: 0.9367
Epoch: [ 0] [  186/  468] time: 12.1453, train_loss: 0.26704201, train_accuracy: 0.9219, test_Accuracy: 0.9331
Epoch: [ 0] [  187/  468] time: 12.2093, train_loss: 0.30581164, train_accuracy: 0.9141, test_Accuracy: 0.9358
Epoch: [ 0] [  188/  468] time: 12.2723, train_loss: 0.26988789, train_accuracy: 0.8984, test_Accuracy: 0.9365
Epoch: [ 0] [  189/  468] time: 12.3363, train_loss: 0.28147525, train_accuracy: 0.9297, test_Accuracy: 0.9356
Epoch: [ 0] [  190/  468] time: 12.4014, train_loss: 0.20998138, train_accuracy: 0.9688, test_Accuracy: 0.9353
Epoch: [ 0] [  191/  468] time: 12.4654, train_loss: 0.16531554, train_accuracy: 0.9453, test_Accuracy: 0.9355
Epoch: [ 0] [  192/  468] time: 12.5284, train_loss: 0.16638854, train_accuracy: 0.9766, test_Accuracy: 0.9364
Epoch: [ 0] [  193/  468] time: 12.5914, train_loss: 0.14850360, train_accuracy: 0.9609, test_Accuracy: 0.9376
Epoch: [ 0] [  194/  468] time: 12.6544, train_loss: 0.30568868, train_accuracy: 0.9062, test_Accuracy: 0.9387
Epoch: [ 0] [  195/  468] time: 12.7184, train_loss: 0.12627041, train_accuracy: 0.9609, test_Accuracy: 0.9414
Epoch: [ 0] [  196/  468] time: 12.7825, train_loss: 0.23984389, train_accuracy: 0.9609, test_Accuracy: 0.9422
Epoch: [ 0] [  197/  468] time: 12.8475, train_loss: 0.16382484, train_accuracy: 0.9531, test_Accuracy: 0.9436
Epoch: [ 0] [  198/  468] time: 12.9115, train_loss: 0.12727252, train_accuracy: 0.9688, test_Accuracy: 0.9436
Epoch: [ 0] [  199/  468] time: 12.9756, train_loss: 0.24766417, train_accuracy: 0.9297, test_Accuracy: 0.9425
Epoch: [ 0] [  200/  468] time: 13.0385, train_loss: 0.24216126, train_accuracy: 0.9375, test_Accuracy: 0.9402
Epoch: [ 0] [  201/  468] time: 13.1025, train_loss: 0.19451016, train_accuracy: 0.9375, test_Accuracy: 0.9380
Epoch: [ 0] [  202/  468] time: 13.1655, train_loss: 0.09552706, train_accuracy: 0.9688, test_Accuracy: 0.9388
Epoch: [ 0] [  203/  468] time: 13.2286, train_loss: 0.20676467, train_accuracy: 0.9219, test_Accuracy: 0.9388
Epoch: [ 0] [  204/  468] time: 13.2916, train_loss: 0.16558582, train_accuracy: 0.9453, test_Accuracy: 0.9411
Epoch: [ 0] [  205/  468] time: 13.3556, train_loss: 0.17059493, train_accuracy: 0.9531, test_Accuracy: 0.9411
Epoch: [ 0] [  206/  468] time: 13.4206, train_loss: 0.11008885, train_accuracy: 0.9609, test_Accuracy: 0.9413
Epoch: [ 0] [  207/  468] time: 13.4846, train_loss: 0.15926999, train_accuracy: 0.9531, test_Accuracy: 0.9399
Epoch: [ 0] [  208/  468] time: 13.5477, train_loss: 0.26672536, train_accuracy: 0.9219, test_Accuracy: 0.9396
Epoch: [ 0] [  209/  468] time: 13.6117, train_loss: 0.23134579, train_accuracy: 0.9375, test_Accuracy: 0.9401
Epoch: [ 0] [  210/  468] time: 13.6748, train_loss: 0.15418190, train_accuracy: 0.9453, test_Accuracy: 0.9397
Epoch: [ 0] [  211/  468] time: 13.7388, train_loss: 0.18166092, train_accuracy: 0.9375, test_Accuracy: 0.9410
Epoch: [ 0] [  212/  468] time: 13.8028, train_loss: 0.20516403, train_accuracy: 0.9219, test_Accuracy: 0.9426
Epoch: [ 0] [  213/  468] time: 13.8688, train_loss: 0.21677539, train_accuracy: 0.9219, test_Accuracy: 0.9442
Epoch: [ 0] [  214/  468] time: 13.9348, train_loss: 0.22261241, train_accuracy: 0.9375, test_Accuracy: 0.9463
Epoch: [ 0] [  215/  468] time: 13.9988, train_loss: 0.34383842, train_accuracy: 0.8828, test_Accuracy: 0.9467
Epoch: [ 0] [  216/  468] time: 14.0658, train_loss: 0.23152712, train_accuracy: 0.9219, test_Accuracy: 0.9456
Epoch: [ 0] [  217/  468] time: 14.1299, train_loss: 0.21360737, train_accuracy: 0.9453, test_Accuracy: 0.9440
Epoch: [ 0] [  218/  468] time: 14.1959, train_loss: 0.14919339, train_accuracy: 0.9609, test_Accuracy: 0.9421
Epoch: [ 0] [  219/  468] time: 14.2629, train_loss: 0.09273322, train_accuracy: 0.9766, test_Accuracy: 0.9408
Epoch: [ 0] [  220/  468] time: 14.3319, train_loss: 0.15447523, train_accuracy: 0.9531, test_Accuracy: 0.9409
Epoch: [ 0] [  221/  468] time: 14.3979, train_loss: 0.27789184, train_accuracy: 0.9141, test_Accuracy: 0.9410
Epoch: [ 0] [  222/  468] time: 14.4629, train_loss: 0.12793493, train_accuracy: 0.9609, test_Accuracy: 0.9424
Epoch: [ 0] [  223/  468] time: 14.5269, train_loss: 0.12226766, train_accuracy: 0.9766, test_Accuracy: 0.9422
Epoch: [ 0] [  224/  468] time: 14.5910, train_loss: 0.13145107, train_accuracy: 0.9688, test_Accuracy: 0.9421
Epoch: [ 0] [  225/  468] time: 14.6580, train_loss: 0.17955813, train_accuracy: 0.9531, test_Accuracy: 0.9405
Epoch: [ 0] [  226/  468] time: 14.7220, train_loss: 0.22709191, train_accuracy: 0.9297, test_Accuracy: 0.9407
Epoch: [ 0] [  227/  468] time: 14.7860, train_loss: 0.22195145, train_accuracy: 0.9531, test_Accuracy: 0.9405
Epoch: [ 0] [  228/  468] time: 14.8490, train_loss: 0.19860703, train_accuracy: 0.9453, test_Accuracy: 0.9406
Epoch: [ 0] [  229/  468] time: 14.9150, train_loss: 0.20411161, train_accuracy: 0.9219, test_Accuracy: 0.9423
Epoch: [ 0] [  230/  468] time: 14.9800, train_loss: 0.17807995, train_accuracy: 0.9297, test_Accuracy: 0.9430
Epoch: [ 0] [  231/  468] time: 15.0431, train_loss: 0.16782898, train_accuracy: 0.9453, test_Accuracy: 0.9440
Epoch: [ 0] [  232/  468] time: 15.1071, train_loss: 0.08167590, train_accuracy: 0.9844, test_Accuracy: 0.9449
Epoch: [ 0] [  233/  468] time: 15.1701, train_loss: 0.17822459, train_accuracy: 0.9375, test_Accuracy: 0.9439
Epoch: [ 0] [  234/  468] time: 15.2331, train_loss: 0.22350088, train_accuracy: 0.9219, test_Accuracy: 0.9419
Epoch: [ 0] [  235/  468] time: 15.2981, train_loss: 0.15869054, train_accuracy: 0.9531, test_Accuracy: 0.9411
Epoch: [ 0] [  236/  468] time: 15.3631, train_loss: 0.06859242, train_accuracy: 0.9766, test_Accuracy: 0.9419
Epoch: [ 0] [  237/  468] time: 15.4251, train_loss: 0.30197757, train_accuracy: 0.8984, test_Accuracy: 0.9438
Epoch: [ 0] [  238/  468] time: 15.4902, train_loss: 0.11942769, train_accuracy: 0.9688, test_Accuracy: 0.9457
Epoch: [ 0] [  239/  468] time: 15.5532, train_loss: 0.15499094, train_accuracy: 0.9609, test_Accuracy: 0.9465
Epoch: [ 0] [  240/  468] time: 15.6162, train_loss: 0.23184153, train_accuracy: 0.9062, test_Accuracy: 0.9455
Epoch: [ 0] [  241/  468] time: 15.6802, train_loss: 0.24996555, train_accuracy: 0.9375, test_Accuracy: 0.9450
Epoch: [ 0] [  242/  468] time: 15.7462, train_loss: 0.11802086, train_accuracy: 0.9531, test_Accuracy: 0.9456
Epoch: [ 0] [  243/  468] time: 15.8092, train_loss: 0.26565617, train_accuracy: 0.9297, test_Accuracy: 0.9463
Epoch: [ 0] [  244/  468] time: 15.8733, train_loss: 0.14965780, train_accuracy: 0.9531, test_Accuracy: 0.9442
Epoch: [ 0] [  245/  468] time: 15.9403, train_loss: 0.18698113, train_accuracy: 0.9375, test_Accuracy: 0.9439
Epoch: [ 0] [  246/  468] time: 16.0043, train_loss: 0.15558021, train_accuracy: 0.9531, test_Accuracy: 0.9433
Epoch: [ 0] [  247/  468] time: 16.0703, train_loss: 0.14589940, train_accuracy: 0.9531, test_Accuracy: 0.9439
Epoch: [ 0] [  248/  468] time: 16.1383, train_loss: 0.18045065, train_accuracy: 0.9375, test_Accuracy: 0.9416
Epoch: [ 0] [  249/  468] time: 16.2023, train_loss: 0.18498233, train_accuracy: 0.9375, test_Accuracy: 0.9415
Epoch: [ 0] [  250/  468] time: 16.2663, train_loss: 0.23034607, train_accuracy: 0.9297, test_Accuracy: 0.9418
Epoch: [ 0] [  251/  468] time: 16.3344, train_loss: 0.10552325, train_accuracy: 0.9688, test_Accuracy: 0.9418
Epoch: [ 0] [  252/  468] time: 16.4004, train_loss: 0.17797375, train_accuracy: 0.9688, test_Accuracy: 0.9433
Epoch: [ 0] [  253/  468] time: 16.4654, train_loss: 0.11630102, train_accuracy: 0.9688, test_Accuracy: 0.9450
Epoch: [ 0] [  254/  468] time: 16.5294, train_loss: 0.14214271, train_accuracy: 0.9297, test_Accuracy: 0.9455
Epoch: [ 0] [  255/  468] time: 16.5914, train_loss: 0.09587899, train_accuracy: 0.9766, test_Accuracy: 0.9453
Epoch: [ 0] [  256/  468] time: 16.6564, train_loss: 0.11949618, train_accuracy: 0.9688, test_Accuracy: 0.9406
Epoch: [ 0] [  257/  468] time: 16.7214, train_loss: 0.19924688, train_accuracy: 0.9219, test_Accuracy: 0.9391
Epoch: [ 0] [  258/  468] time: 16.7845, train_loss: 0.15476713, train_accuracy: 0.9531, test_Accuracy: 0.9396
Epoch: [ 0] [  259/  468] time: 16.8485, train_loss: 0.13927916, train_accuracy: 0.9688, test_Accuracy: 0.9433
Epoch: [ 0] [  260/  468] time: 16.9125, train_loss: 0.11039710, train_accuracy: 0.9688, test_Accuracy: 0.9464
Epoch: [ 0] [  261/  468] time: 16.9745, train_loss: 0.28463781, train_accuracy: 0.9219, test_Accuracy: 0.9484
Epoch: [ 0] [  262/  468] time: 17.0385, train_loss: 0.19300835, train_accuracy: 0.9531, test_Accuracy: 0.9499
Epoch: [ 0] [  263/  468] time: 17.1015, train_loss: 0.17742682, train_accuracy: 0.9531, test_Accuracy: 0.9480
Epoch: [ 0] [  264/  468] time: 17.1635, train_loss: 0.11956368, train_accuracy: 0.9531, test_Accuracy: 0.9458
Epoch: [ 0] [  265/  468] time: 17.2256, train_loss: 0.10494197, train_accuracy: 0.9688, test_Accuracy: 0.9435
Epoch: [ 0] [  266/  468] time: 17.2896, train_loss: 0.14761403, train_accuracy: 0.9531, test_Accuracy: 0.9434
Epoch: [ 0] [  267/  468] time: 17.3516, train_loss: 0.13441488, train_accuracy: 0.9609, test_Accuracy: 0.9451
Epoch: [ 0] [  268/  468] time: 17.4136, train_loss: 0.11155730, train_accuracy: 0.9922, test_Accuracy: 0.9481
Epoch: [ 0] [  269/  468] time: 17.4756, train_loss: 0.19391273, train_accuracy: 0.9688, test_Accuracy: 0.9492
Epoch: [ 0] [  270/  468] time: 17.5386, train_loss: 0.26175904, train_accuracy: 0.9375, test_Accuracy: 0.9490
Epoch: [ 0] [  271/  468] time: 17.6016, train_loss: 0.18650766, train_accuracy: 0.9297, test_Accuracy: 0.9487
Epoch: [ 0] [  272/  468] time: 17.6667, train_loss: 0.17990604, train_accuracy: 0.9375, test_Accuracy: 0.9469
Epoch: [ 0] [  273/  468] time: 17.7317, train_loss: 0.12978739, train_accuracy: 0.9688, test_Accuracy: 0.9459
Epoch: [ 0] [  274/  468] time: 17.7957, train_loss: 0.08045278, train_accuracy: 0.9922, test_Accuracy: 0.9446
Epoch: [ 0] [  275/  468] time: 17.8587, train_loss: 0.13658679, train_accuracy: 0.9688, test_Accuracy: 0.9462
Epoch: [ 0] [  276/  468] time: 17.9267, train_loss: 0.10277054, train_accuracy: 0.9766, test_Accuracy: 0.9473
Epoch: [ 0] [  277/  468] time: 17.9897, train_loss: 0.15788171, train_accuracy: 0.9766, test_Accuracy: 0.9491
Epoch: [ 0] [  278/  468] time: 18.0548, train_loss: 0.19351265, train_accuracy: 0.9062, test_Accuracy: 0.9494
Epoch: [ 0] [  279/  468] time: 18.1228, train_loss: 0.21694133, train_accuracy: 0.9062, test_Accuracy: 0.9513
Epoch: [ 0] [  280/  468] time: 18.1898, train_loss: 0.33667937, train_accuracy: 0.9297, test_Accuracy: 0.9521
Epoch: [ 0] [  281/  468] time: 18.2548, train_loss: 0.15434639, train_accuracy: 0.9531, test_Accuracy: 0.9510
Epoch: [ 0] [  282/  468] time: 18.3228, train_loss: 0.11569065, train_accuracy: 0.9531, test_Accuracy: 0.9508
Epoch: [ 0] [  283/  468] time: 18.3888, train_loss: 0.14032760, train_accuracy: 0.9531, test_Accuracy: 0.9518
Epoch: [ 0] [  284/  468] time: 18.4558, train_loss: 0.18152231, train_accuracy: 0.9297, test_Accuracy: 0.9503
Epoch: [ 0] [  285/  468] time: 18.5209, train_loss: 0.09862983, train_accuracy: 0.9766, test_Accuracy: 0.9504
Epoch: [ 0] [  286/  468] time: 18.5919, train_loss: 0.12200639, train_accuracy: 0.9688, test_Accuracy: 0.9474
Epoch: [ 0] [  287/  468] time: 18.6559, train_loss: 0.22918737, train_accuracy: 0.9141, test_Accuracy: 0.9476
Epoch: [ 0] [  288/  468] time: 18.7239, train_loss: 0.19751920, train_accuracy: 0.9375, test_Accuracy: 0.9502
Epoch: [ 0] [  289/  468] time: 18.7899, train_loss: 0.28085297, train_accuracy: 0.9141, test_Accuracy: 0.9508
Epoch: [ 0] [  290/  468] time: 18.8539, train_loss: 0.10131221, train_accuracy: 0.9609, test_Accuracy: 0.9522
Epoch: [ 0] [  291/  468] time: 18.9180, train_loss: 0.19732203, train_accuracy: 0.9219, test_Accuracy: 0.9529
Epoch: [ 0] [  292/  468] time: 18.9840, train_loss: 0.07863627, train_accuracy: 0.9844, test_Accuracy: 0.9527
Epoch: [ 0] [  293/  468] time: 19.0480, train_loss: 0.15197501, train_accuracy: 0.9531, test_Accuracy: 0.9524
Epoch: [ 0] [  294/  468] time: 19.1100, train_loss: 0.16639140, train_accuracy: 0.9609, test_Accuracy: 0.9526
Epoch: [ 0] [  295/  468] time: 19.1750, train_loss: 0.18607783, train_accuracy: 0.9297, test_Accuracy: 0.9523
Epoch: [ 0] [  296/  468] time: 19.2390, train_loss: 0.16796342, train_accuracy: 0.9531, test_Accuracy: 0.9523
Epoch: [ 0] [  297/  468] time: 19.3020, train_loss: 0.17327395, train_accuracy: 0.9375, test_Accuracy: 0.9519
Epoch: [ 0] [  298/  468] time: 19.3651, train_loss: 0.16989313, train_accuracy: 0.9609, test_Accuracy: 0.9518
Epoch: [ 0] [  299/  468] time: 19.4281, train_loss: 0.21625620, train_accuracy: 0.9297, test_Accuracy: 0.9520
Epoch: [ 0] [  300/  468] time: 19.4911, train_loss: 0.29546732, train_accuracy: 0.9297, test_Accuracy: 0.9531
Epoch: [ 0] [  301/  468] time: 19.5561, train_loss: 0.14657137, train_accuracy: 0.9531, test_Accuracy: 0.9540
Epoch: [ 0] [  302/  468] time: 19.6191, train_loss: 0.20857713, train_accuracy: 0.9219, test_Accuracy: 0.9521
Epoch: [ 0] [  303/  468] time: 19.6811, train_loss: 0.25434366, train_accuracy: 0.9297, test_Accuracy: 0.9509
Epoch: [ 0] [  304/  468] time: 19.7441, train_loss: 0.11656755, train_accuracy: 0.9531, test_Accuracy: 0.9489
Epoch: [ 0] [  305/  468] time: 19.8082, train_loss: 0.11812200, train_accuracy: 0.9609, test_Accuracy: 0.9468
Epoch: [ 0] [  306/  468] time: 19.8702, train_loss: 0.21424091, train_accuracy: 0.9297, test_Accuracy: 0.9451
Epoch: [ 0] [  307/  468] time: 19.9332, train_loss: 0.12282729, train_accuracy: 0.9609, test_Accuracy: 0.9451
Epoch: [ 0] [  308/  468] time: 19.9952, train_loss: 0.25347343, train_accuracy: 0.9297, test_Accuracy: 0.9472
Epoch: [ 0] [  309/  468] time: 20.0562, train_loss: 0.12584005, train_accuracy: 0.9766, test_Accuracy: 0.9504
Epoch: [ 0] [  310/  468] time: 20.1192, train_loss: 0.17315902, train_accuracy: 0.9375, test_Accuracy: 0.9515
Epoch: [ 0] [  311/  468] time: 20.1812, train_loss: 0.12967509, train_accuracy: 0.9531, test_Accuracy: 0.9527
Epoch: [ 0] [  312/  468] time: 20.2463, train_loss: 0.16925472, train_accuracy: 0.9531, test_Accuracy: 0.9510
Epoch: [ 0] [  313/  468] time: 20.3103, train_loss: 0.15002504, train_accuracy: 0.9531, test_Accuracy: 0.9493
Epoch: [ 0] [  314/  468] time: 20.3763, train_loss: 0.08000503, train_accuracy: 0.9766, test_Accuracy: 0.9465
Epoch: [ 0] [  315/  468] time: 20.4403, train_loss: 0.17883195, train_accuracy: 0.9297, test_Accuracy: 0.9474
Epoch: [ 0] [  316/  468] time: 20.5043, train_loss: 0.20756245, train_accuracy: 0.9453, test_Accuracy: 0.9502
Epoch: [ 0] [  317/  468] time: 20.5683, train_loss: 0.17249253, train_accuracy: 0.9297, test_Accuracy: 0.9516
Epoch: [ 0] [  318/  468] time: 20.6313, train_loss: 0.13240860, train_accuracy: 0.9609, test_Accuracy: 0.9509
Epoch: [ 0] [  319/  468] time: 20.6954, train_loss: 0.18395954, train_accuracy: 0.9375, test_Accuracy: 0.9494
Epoch: [ 0] [  320/  468] time: 20.7594, train_loss: 0.16948792, train_accuracy: 0.9688, test_Accuracy: 0.9466
Epoch: [ 0] [  321/  468] time: 20.8224, train_loss: 0.17623082, train_accuracy: 0.9531, test_Accuracy: 0.9446
Epoch: [ 0] [  322/  468] time: 20.8864, train_loss: 0.17252052, train_accuracy: 0.9453, test_Accuracy: 0.9455
Epoch: [ 0] [  323/  468] time: 20.9504, train_loss: 0.12580900, train_accuracy: 0.9609, test_Accuracy: 0.9466
Epoch: [ 0] [  324/  468] time: 21.0126, train_loss: 0.24108915, train_accuracy: 0.9219, test_Accuracy: 0.9508
Epoch: [ 0] [  325/  468] time: 21.0784, train_loss: 0.13873923, train_accuracy: 0.9453, test_Accuracy: 0.9524
Epoch: [ 0] [  326/  468] time: 21.1445, train_loss: 0.13623059, train_accuracy: 0.9688, test_Accuracy: 0.9529
Epoch: [ 0] [  327/  468] time: 21.2095, train_loss: 0.10226237, train_accuracy: 0.9766, test_Accuracy: 0.9510
Epoch: [ 0] [  328/  468] time: 21.2740, train_loss: 0.19152004, train_accuracy: 0.9609, test_Accuracy: 0.9482
Epoch: [ 0] [  329/  468] time: 21.3380, train_loss: 0.14426246, train_accuracy: 0.9609, test_Accuracy: 0.9474
Epoch: [ 0] [  330/  468] time: 21.4020, train_loss: 0.18879429, train_accuracy: 0.9297, test_Accuracy: 0.9478
Epoch: [ 0] [  331/  468] time: 21.4670, train_loss: 0.11458261, train_accuracy: 0.9688, test_Accuracy: 0.9500
Epoch: [ 0] [  332/  468] time: 21.5870, train_loss: 0.23528746, train_accuracy: 0.9297, test_Accuracy: 0.9528
Epoch: [ 0] [  333/  468] time: 21.6530, train_loss: 0.15576802, train_accuracy: 0.9375, test_Accuracy: 0.9546
Epoch: [ 0] [  334/  468] time: 21.7180, train_loss: 0.16457088, train_accuracy: 0.9531, test_Accuracy: 0.9550
Epoch: [ 0] [  335/  468] time: 21.7820, train_loss: 0.14703712, train_accuracy: 0.9609, test_Accuracy: 0.9538
Epoch: [ 0] [  336/  468] time: 21.8461, train_loss: 0.13901797, train_accuracy: 0.9531, test_Accuracy: 0.9540
Epoch: [ 0] [  337/  468] time: 21.9111, train_loss: 0.15841904, train_accuracy: 0.9609, test_Accuracy: 0.9540
Epoch: [ 0] [  338/  468] time: 21.9751, train_loss: 0.08693589, train_accuracy: 0.9688, test_Accuracy: 0.9548
Epoch: [ 0] [  339/  468] time: 22.0391, train_loss: 0.12024122, train_accuracy: 0.9766, test_Accuracy: 0.9547
Epoch: [ 0] [  340/  468] time: 22.1041, train_loss: 0.18121222, train_accuracy: 0.9531, test_Accuracy: 0.9552
Epoch: [ 0] [  341/  468] time: 22.1701, train_loss: 0.20300639, train_accuracy: 0.9531, test_Accuracy: 0.9556
Epoch: [ 0] [  342/  468] time: 22.2331, train_loss: 0.16562158, train_accuracy: 0.9609, test_Accuracy: 0.9552
Epoch: [ 0] [  343/  468] time: 22.2972, train_loss: 0.18433744, train_accuracy: 0.9375, test_Accuracy: 0.9565
Epoch: [ 0] [  344/  468] time: 22.3612, train_loss: 0.16098902, train_accuracy: 0.9609, test_Accuracy: 0.9570
Epoch: [ 0] [  345/  468] time: 22.4252, train_loss: 0.29687661, train_accuracy: 0.9062, test_Accuracy: 0.9583
Epoch: [ 0] [  346/  468] time: 22.4902, train_loss: 0.13536343, train_accuracy: 0.9609, test_Accuracy: 0.9577
Epoch: [ 0] [  347/  468] time: 22.5542, train_loss: 0.16808861, train_accuracy: 0.9453, test_Accuracy: 0.9580
Epoch: [ 0] [  348/  468] time: 22.6182, train_loss: 0.13764171, train_accuracy: 0.9844, test_Accuracy: 0.9577
Epoch: [ 0] [  349/  468] time: 22.6833, train_loss: 0.11232210, train_accuracy: 0.9609, test_Accuracy: 0.9564
Epoch: [ 0] [  350/  468] time: 22.7463, train_loss: 0.14690028, train_accuracy: 0.9375, test_Accuracy: 0.9558
Epoch: [ 0] [  351/  468] time: 22.8113, train_loss: 0.17780462, train_accuracy: 0.9531, test_Accuracy: 0.9556
Epoch: [ 0] [  352/  468] time: 22.8753, train_loss: 0.14793049, train_accuracy: 0.9609, test_Accuracy: 0.9550
Epoch: [ 0] [  353/  468] time: 22.9393, train_loss: 0.20168084, train_accuracy: 0.9531, test_Accuracy: 0.9547
Epoch: [ 0] [  354/  468] time: 23.0033, train_loss: 0.14828789, train_accuracy: 0.9453, test_Accuracy: 0.9543
Epoch: [ 0] [  355/  468] time: 23.0663, train_loss: 0.20324868, train_accuracy: 0.9531, test_Accuracy: 0.9555
Epoch: [ 0] [  356/  468] time: 23.1294, train_loss: 0.15619661, train_accuracy: 0.9609, test_Accuracy: 0.9560
Epoch: [ 0] [  357/  468] time: 23.1924, train_loss: 0.20183887, train_accuracy: 0.9375, test_Accuracy: 0.9569
Epoch: [ 0] [  358/  468] time: 23.2574, train_loss: 0.15836586, train_accuracy: 0.9609, test_Accuracy: 0.9571
Epoch: [ 0] [  359/  468] time: 23.3214, train_loss: 0.16267470, train_accuracy: 0.9453, test_Accuracy: 0.9584
Epoch: [ 0] [  360/  468] time: 23.3864, train_loss: 0.13085663, train_accuracy: 0.9609, test_Accuracy: 0.9578
Epoch: [ 0] [  361/  468] time: 23.4504, train_loss: 0.18066928, train_accuracy: 0.9453, test_Accuracy: 0.9572
Epoch: [ 0] [  362/  468] time: 23.5141, train_loss: 0.20114744, train_accuracy: 0.9297, test_Accuracy: 0.9573
Epoch: [ 0] [  363/  468] time: 23.5755, train_loss: 0.11035044, train_accuracy: 0.9688, test_Accuracy: 0.9565
Epoch: [ 0] [  364/  468] time: 23.6385, train_loss: 0.14055173, train_accuracy: 0.9531, test_Accuracy: 0.9570
Epoch: [ 0] [  365/  468] time: 23.7016, train_loss: 0.15765198, train_accuracy: 0.9688, test_Accuracy: 0.9576
Epoch: [ 0] [  366/  468] time: 23.7646, train_loss: 0.14929019, train_accuracy: 0.9531, test_Accuracy: 0.9586
Epoch: [ 0] [  367/  468] time: 23.8300, train_loss: 0.28184396, train_accuracy: 0.9219, test_Accuracy: 0.9601
Epoch: [ 0] [  368/  468] time: 23.8940, train_loss: 0.12710188, train_accuracy: 0.9531, test_Accuracy: 0.9597
Epoch: [ 0] [  369/  468] time: 23.9570, train_loss: 0.07625520, train_accuracy: 0.9922, test_Accuracy: 0.9592
Epoch: [ 0] [  370/  468] time: 24.0250, train_loss: 0.10960338, train_accuracy: 0.9688, test_Accuracy: 0.9588
Epoch: [ 0] [  371/  468] time: 24.0890, train_loss: 0.08890978, train_accuracy: 0.9766, test_Accuracy: 0.9581
Epoch: [ 0] [  372/  468] time: 24.1520, train_loss: 0.07581397, train_accuracy: 0.9844, test_Accuracy: 0.9579
Epoch: [ 0] [  373/  468] time: 24.2180, train_loss: 0.15715739, train_accuracy: 0.9688, test_Accuracy: 0.9586
Epoch: [ 0] [  374/  468] time: 24.2815, train_loss: 0.09676296, train_accuracy: 0.9844, test_Accuracy: 0.9600
Epoch: [ 0] [  375/  468] time: 24.3465, train_loss: 0.11426444, train_accuracy: 0.9688, test_Accuracy: 0.9601
Epoch: [ 0] [  376/  468] time: 24.4115, train_loss: 0.19789585, train_accuracy: 0.9375, test_Accuracy: 0.9598
Epoch: [ 0] [  377/  468] time: 24.4755, train_loss: 0.13910045, train_accuracy: 0.9531, test_Accuracy: 0.9587
Epoch: [ 0] [  378/  468] time: 24.5420, train_loss: 0.10982578, train_accuracy: 0.9609, test_Accuracy: 0.9579
Epoch: [ 0] [  379/  468] time: 24.6084, train_loss: 0.11757764, train_accuracy: 0.9844, test_Accuracy: 0.9561
Epoch: [ 0] [  380/  468] time: 24.6744, train_loss: 0.11057130, train_accuracy: 0.9609, test_Accuracy: 0.9529
Epoch: [ 0] [  381/  468] time: 24.7404, train_loss: 0.13472016, train_accuracy: 0.9531, test_Accuracy: 0.9529
Epoch: [ 0] [  382/  468] time: 24.8054, train_loss: 0.14099713, train_accuracy: 0.9609, test_Accuracy: 0.9538
Epoch: [ 0] [  383/  468] time: 24.8704, train_loss: 0.13744125, train_accuracy: 0.9688, test_Accuracy: 0.9554
Epoch: [ 0] [  384/  468] time: 24.9348, train_loss: 0.21594217, train_accuracy: 0.9453, test_Accuracy: 0.9560
Epoch: [ 0] [  385/  468] time: 24.9998, train_loss: 0.11624073, train_accuracy: 0.9531, test_Accuracy: 0.9576
Epoch: [ 0] [  386/  468] time: 25.0639, train_loss: 0.11062561, train_accuracy: 0.9688, test_Accuracy: 0.9578
Epoch: [ 0] [  387/  468] time: 25.1289, train_loss: 0.08605760, train_accuracy: 0.9609, test_Accuracy: 0.9577
Epoch: [ 0] [  388/  468] time: 25.1929, train_loss: 0.06960788, train_accuracy: 0.9766, test_Accuracy: 0.9568
Epoch: [ 0] [  389/  468] time: 25.2579, train_loss: 0.14723164, train_accuracy: 0.9531, test_Accuracy: 0.9564
Epoch: [ 0] [  390/  468] time: 25.3219, train_loss: 0.17202045, train_accuracy: 0.9453, test_Accuracy: 0.9560
Epoch: [ 0] [  391/  468] time: 25.3869, train_loss: 0.13020836, train_accuracy: 0.9609, test_Accuracy: 0.9567
Epoch: [ 0] [  392/  468] time: 25.4510, train_loss: 0.18430941, train_accuracy: 0.9375, test_Accuracy: 0.9561
Epoch: [ 0] [  393/  468] time: 25.5155, train_loss: 0.11469187, train_accuracy: 0.9609, test_Accuracy: 0.9557
Epoch: [ 0] [  394/  468] time: 25.5794, train_loss: 0.11584131, train_accuracy: 0.9609, test_Accuracy: 0.9563
Epoch: [ 0] [  395/  468] time: 25.6516, train_loss: 0.23650636, train_accuracy: 0.9375, test_Accuracy: 0.9564
Epoch: [ 0] [  396/  468] time: 25.7157, train_loss: 0.13211471, train_accuracy: 0.9609, test_Accuracy: 0.9569
Epoch: [ 0] [  397/  468] time: 25.7784, train_loss: 0.09262250, train_accuracy: 0.9766, test_Accuracy: 0.9564
Epoch: [ 0] [  398/  468] time: 25.8424, train_loss: 0.17458144, train_accuracy: 0.9375, test_Accuracy: 0.9574
Epoch: [ 0] [  399/  468] time: 25.9054, train_loss: 0.15859000, train_accuracy: 0.9453, test_Accuracy: 0.9573
Epoch: [ 0] [  400/  468] time: 25.9704, train_loss: 0.15582328, train_accuracy: 0.9609, test_Accuracy: 0.9587
Epoch: [ 0] [  401/  468] time: 26.0325, train_loss: 0.05083877, train_accuracy: 0.9922, test_Accuracy: 0.9591
Epoch: [ 0] [  402/  468] time: 26.0955, train_loss: 0.19545192, train_accuracy: 0.9375, test_Accuracy: 0.9592
Epoch: [ 0] [  403/  468] time: 26.1575, train_loss: 0.18975025, train_accuracy: 0.9297, test_Accuracy: 0.9600
Epoch: [ 0] [  404/  468] time: 26.2205, train_loss: 0.13589118, train_accuracy: 0.9609, test_Accuracy: 0.9603
Epoch: [ 0] [  405/  468] time: 26.2845, train_loss: 0.21268882, train_accuracy: 0.9609, test_Accuracy: 0.9585
Epoch: [ 0] [  406/  468] time: 26.3475, train_loss: 0.14337090, train_accuracy: 0.9609, test_Accuracy: 0.9566
Epoch: [ 0] [  407/  468] time: 26.4105, train_loss: 0.14414740, train_accuracy: 0.9609, test_Accuracy: 0.9554
Epoch: [ 0] [  408/  468] time: 26.4766, train_loss: 0.13706176, train_accuracy: 0.9609, test_Accuracy: 0.9536
Epoch: [ 0] [  409/  468] time: 26.5396, train_loss: 0.13669115, train_accuracy: 0.9531, test_Accuracy: 0.9512
Epoch: [ 0] [  410/  468] time: 26.6056, train_loss: 0.15882169, train_accuracy: 0.9531, test_Accuracy: 0.9516
Epoch: [ 0] [  411/  468] time: 26.6686, train_loss: 0.07023047, train_accuracy: 0.9844, test_Accuracy: 0.9521
Epoch: [ 0] [  412/  468] time: 26.7316, train_loss: 0.08542548, train_accuracy: 0.9688, test_Accuracy: 0.9531
Epoch: [ 0] [  413/  468] time: 26.7956, train_loss: 0.26154473, train_accuracy: 0.9141, test_Accuracy: 0.9557
Epoch: [ 0] [  414/  468] time: 26.8587, train_loss: 0.14225608, train_accuracy: 0.9531, test_Accuracy: 0.9558
Epoch: [ 0] [  415/  468] time: 26.9237, train_loss: 0.13583456, train_accuracy: 0.9297, test_Accuracy: 0.9546
Epoch: [ 0] [  416/  468] time: 26.9877, train_loss: 0.07992653, train_accuracy: 0.9766, test_Accuracy: 0.9523
Epoch: [ 0] [  417/  468] time: 27.0517, train_loss: 0.17846315, train_accuracy: 0.9297, test_Accuracy: 0.9511
Epoch: [ 0] [  418/  468] time: 27.1147, train_loss: 0.15516707, train_accuracy: 0.9375, test_Accuracy: 0.9499
Epoch: [ 0] [  419/  468] time: 27.1787, train_loss: 0.13926333, train_accuracy: 0.9531, test_Accuracy: 0.9514
Epoch: [ 0] [  420/  468] time: 27.2417, train_loss: 0.11705200, train_accuracy: 0.9531, test_Accuracy: 0.9552
Epoch: [ 0] [  421/  468] time: 27.3058, train_loss: 0.16251163, train_accuracy: 0.9453, test_Accuracy: 0.9580
Epoch: [ 0] [  422/  468] time: 27.3678, train_loss: 0.15031728, train_accuracy: 0.9453, test_Accuracy: 0.9588
Epoch: [ 0] [  423/  468] time: 27.4298, train_loss: 0.13261396, train_accuracy: 0.9609, test_Accuracy: 0.9615
Epoch: [ 0] [  424/  468] time: 27.4938, train_loss: 0.05896267, train_accuracy: 0.9844, test_Accuracy: 0.9622
Epoch: [ 0] [  425/  468] time: 27.5558, train_loss: 0.13265391, train_accuracy: 0.9688, test_Accuracy: 0.9603
Epoch: [ 0] [  426/  468] time: 27.6178, train_loss: 0.15410823, train_accuracy: 0.9531, test_Accuracy: 0.9589
Epoch: [ 0] [  427/  468] time: 27.6798, train_loss: 0.07289842, train_accuracy: 0.9922, test_Accuracy: 0.9582
Epoch: [ 0] [  428/  468] time: 27.7419, train_loss: 0.17787296, train_accuracy: 0.9453, test_Accuracy: 0.9574
Epoch: [ 0] [  429/  468] time: 27.8059, train_loss: 0.19533101, train_accuracy: 0.9609, test_Accuracy: 0.9583
Epoch: [ 0] [  430/  468] time: 27.9009, train_loss: 0.10289049, train_accuracy: 0.9766, test_Accuracy: 0.9593
Epoch: [ 0] [  431/  468] time: 28.0029, train_loss: 0.12447056, train_accuracy: 0.9531, test_Accuracy: 0.9610
Epoch: [ 0] [  432/  468] time: 28.0689, train_loss: 0.07770907, train_accuracy: 0.9922, test_Accuracy: 0.9610
Epoch: [ 0] [  433/  468] time: 28.1329, train_loss: 0.12110458, train_accuracy: 0.9688, test_Accuracy: 0.9603
Epoch: [ 0] [  434/  468] time: 28.1970, train_loss: 0.08781143, train_accuracy: 0.9688, test_Accuracy: 0.9589
Epoch: [ 0] [  435/  468] time: 28.2630, train_loss: 0.15456277, train_accuracy: 0.9453, test_Accuracy: 0.9577
Epoch: [ 0] [  436/  468] time: 28.3560, train_loss: 0.17653108, train_accuracy: 0.9609, test_Accuracy: 0.9562
Epoch: [ 0] [  437/  468] time: 28.4220, train_loss: 0.13572128, train_accuracy: 0.9844, test_Accuracy: 0.9560
Epoch: [ 0] [  438/  468] time: 28.4880, train_loss: 0.16228831, train_accuracy: 0.9531, test_Accuracy: 0.9569
Epoch: [ 0] [  439/  468] time: 28.5510, train_loss: 0.09951203, train_accuracy: 0.9609, test_Accuracy: 0.9576
Epoch: [ 0] [  440/  468] time: 28.6151, train_loss: 0.13474143, train_accuracy: 0.9531, test_Accuracy: 0.9577
Epoch: [ 0] [  441/  468] time: 28.6791, train_loss: 0.15225090, train_accuracy: 0.9453, test_Accuracy: 0.9589
Epoch: [ 0] [  442/  468] time: 28.7431, train_loss: 0.08897963, train_accuracy: 0.9688, test_Accuracy: 0.9592
Epoch: [ 0] [  443/  468] time: 28.8391, train_loss: 0.12807919, train_accuracy: 0.9609, test_Accuracy: 0.9594
Epoch: [ 0] [  444/  468] time: 28.9041, train_loss: 0.16098553, train_accuracy: 0.9531, test_Accuracy: 0.9590
Epoch: [ 0] [  445/  468] time: 28.9671, train_loss: 0.16510235, train_accuracy: 0.9688, test_Accuracy: 0.9590
Epoch: [ 0] [  446/  468] time: 29.0311, train_loss: 0.08558747, train_accuracy: 0.9688, test_Accuracy: 0.9593
Epoch: [ 0] [  447/  468] time: 29.0962, train_loss: 0.26763219, train_accuracy: 0.9375, test_Accuracy: 0.9597
Epoch: [ 0] [  448/  468] time: 29.1612, train_loss: 0.11790995, train_accuracy: 0.9531, test_Accuracy: 0.9610
Epoch: [ 0] [  449/  468] time: 29.2252, train_loss: 0.15260196, train_accuracy: 0.9453, test_Accuracy: 0.9616
Epoch: [ 0] [  450/  468] time: 29.2912, train_loss: 0.13379526, train_accuracy: 0.9609, test_Accuracy: 0.9626
Epoch: [ 0] [  451/  468] time: 29.3572, train_loss: 0.12205721, train_accuracy: 0.9609, test_Accuracy: 0.9617
Epoch: [ 0] [  452/  468] time: 29.4212, train_loss: 0.15094128, train_accuracy: 0.9609, test_Accuracy: 0.9617
Epoch: [ 0] [  453/  468] time: 29.4842, train_loss: 0.05792763, train_accuracy: 1.0000, test_Accuracy: 0.9605
Epoch: [ 0] [  454/  468] time: 29.5473, train_loss: 0.11666223, train_accuracy: 0.9688, test_Accuracy: 0.9603
Epoch: [ 0] [  455/  468] time: 29.6093, train_loss: 0.05687680, train_accuracy: 0.9844, test_Accuracy: 0.9594
Epoch: [ 0] [  456/  468] time: 29.6713, train_loss: 0.11365558, train_accuracy: 0.9609, test_Accuracy: 0.9581
Epoch: [ 0] [  457/  468] time: 29.7343, train_loss: 0.08995635, train_accuracy: 0.9688, test_Accuracy: 0.9578
Epoch: [ 0] [  458/  468] time: 29.8013, train_loss: 0.15706646, train_accuracy: 0.9609, test_Accuracy: 0.9594
Epoch: [ 0] [  459/  468] time: 29.9063, train_loss: 0.15029000, train_accuracy: 0.9531, test_Accuracy: 0.9622
Epoch: [ 0] [  460/  468] time: 29.9734, train_loss: 0.15182897, train_accuracy: 0.9531, test_Accuracy: 0.9638
Epoch: [ 0] [  461/  468] time: 30.0384, train_loss: 0.09535036, train_accuracy: 0.9688, test_Accuracy: 0.9635
Epoch: [ 0] [  462/  468] time: 30.1014, train_loss: 0.14583090, train_accuracy: 0.9531, test_Accuracy: 0.9621
Epoch: [ 0] [  463/  468] time: 30.1644, train_loss: 0.09659317, train_accuracy: 0.9844, test_Accuracy: 0.9600
Epoch: [ 0] [  464/  468] time: 30.2294, train_loss: 0.07517572, train_accuracy: 0.9766, test_Accuracy: 0.9593
Epoch: [ 0] [  465/  468] time: 30.2944, train_loss: 0.10643730, train_accuracy: 0.9766, test_Accuracy: 0.9589
Epoch: [ 0] [  466/  468] time: 30.3604, train_loss: 0.11571550, train_accuracy: 0.9688, test_Accuracy: 0.9598
Epoch: [ 0] [  467/  468] time: 30.4285, train_loss: 0.12712526, train_accuracy: 0.9688, test_Accuracy: 0.9607
Epoch: [ 0] [  468/  468] time: 30.4955, train_loss: 0.09152033, train_accuracy: 0.9688, test_Accuracy: 0.9618

Out[21]:

'checkpoints\\nn_softmax\\nn_softmax-469-1'

After training, we make a model with training accuracy of 98.9% and test accracy of 97.1%. Also, the checkpoint is generated, so we don't need to train at the beginning of the process, just load the model.

In [22]:

# Restore checkpoint if it exists
could_load, checkpoint_counter = load(model, checkpoint_dir)

if could_load:
    start_epoch = (int)(checkpoint_counter / training_iter)        
    counter = checkpoint_counter        
    print(" [*] Load SUCCESS")
else:
    start_epoch = 0
    start_iteration = 0
    counter = 0
    print(" [!] Load failed...")
    
# train phase
for epoch in range(start_epoch, training_epochs):
    for idx, (train_input, train_label) in enumerate(train_ds):            
        grads = grad(model, train_input, train_label)
        optimizer.apply_gradients(grads_and_vars=zip(grads, model.variables))

        train_loss = loss_fn(model, train_input, train_label)
        train_accuracy = accuracy_fn(model, train_input, train_label)
                
        for test_input, test_label in test_ds:                
            test_accuracy = accuracy_fn(model, test_input, test_label)

        print(
            "Epoch: [%2d] [%5d/%5d] time: %4.4f, train_loss: %.8f, train_accuracy: %.4f, test_Accuracy: %.4f" \
            % (epoch, idx, training_iter, time() - start_time, train_loss, train_accuracy,
           test_accuracy))
        counter += 1                
checkpoint.save(file_prefix=checkpoint_prefix + '-{}'.format(counter))

 [*] Reading checkpoints...
 [*] Success to read nn_softmax-469-1
 [*] Load SUCCESS

Out[22]:

'checkpoints\\nn_softmax\\nn_softmax-469-2'

Weight Initialization¶

The purpose of Gradient Descent is to find the point that minimize the loss.

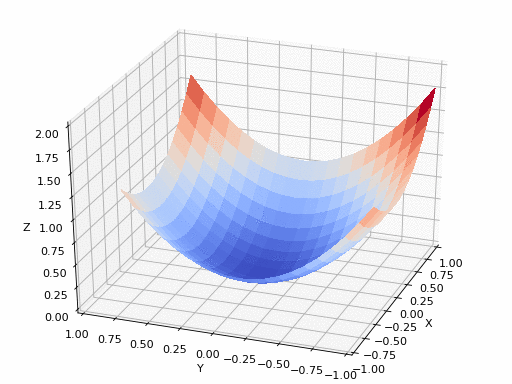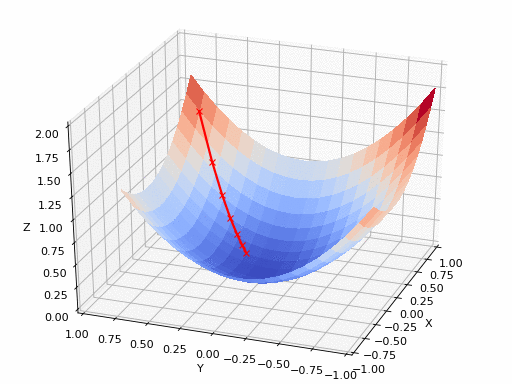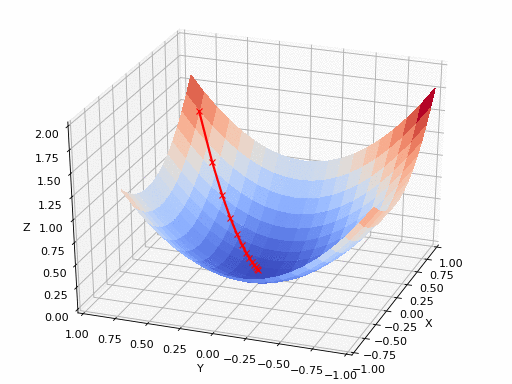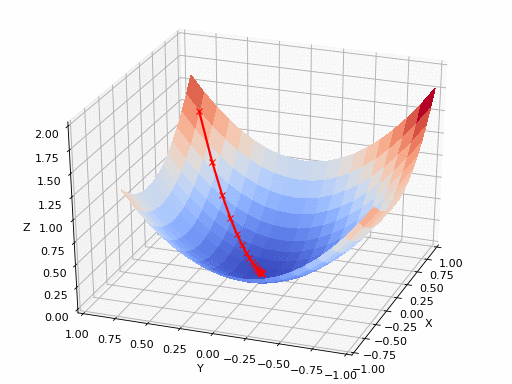
gradient

So in this example, whatever the loss is different with respect to x, y, z, when we apply gradient descent, we can find the minimum point. But what if the loss function space is like this, how can we find the minimum point when we use gradient descent?

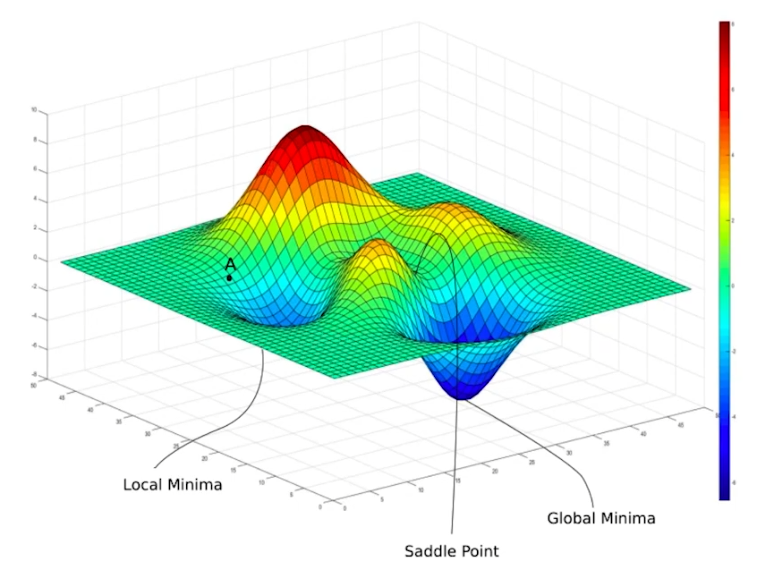
saddle point

Previously, we initialized our weight to sample randomly from normal distribution. But our weight is initialized with $A$, we cannot reach the global minima, just local minima. Or we may stuck in saddle point.

There are many approaches to avoid stucking local minima or saddle point. One of the approaches may be initializing the weight with some rules. Xavier initialization is that kind of things. Instead of sampling from normal distribution, Xavier initialization samples its weight from some distribution that have variance,

$$ Var_{Xe}(W) = \frac{2}{\text{Channel_in} + \text{Channel_out}} $$

As you can see that, the number of channel input and output is related on the weight sampling, it has more probability that can find global minima. For the details, please check this paper.

Note: Tensorflow layer API has weight initialization argument(kernel_initializer). And its default value is glorot_uniform. Actually, Xavier initialization is also called glorot initialization, since the author of paper that introduced xavier initialization is glorot.

He Initialization is another way to initialize weights, especially focused on ReLU activation function. Similar with xavier initialization, he initialization samples its weights from the distribution with variance,

$$ Var_{He}(W) = \frac{4}{\text{Channel_in} + \text{Channel_out}} $$

Code¶

In the previous example, we initialized its weight from normali distribution. If we want to change this to Xavier or He, you can define the weight_init like this,

# Xavier Initializer
weight_init = tf.keras.initializers.glorot_uniform()

# He Initializer
weight init = tf.keras.initializers.he_uniform()

Dropout¶

Suppose we have following three cases,

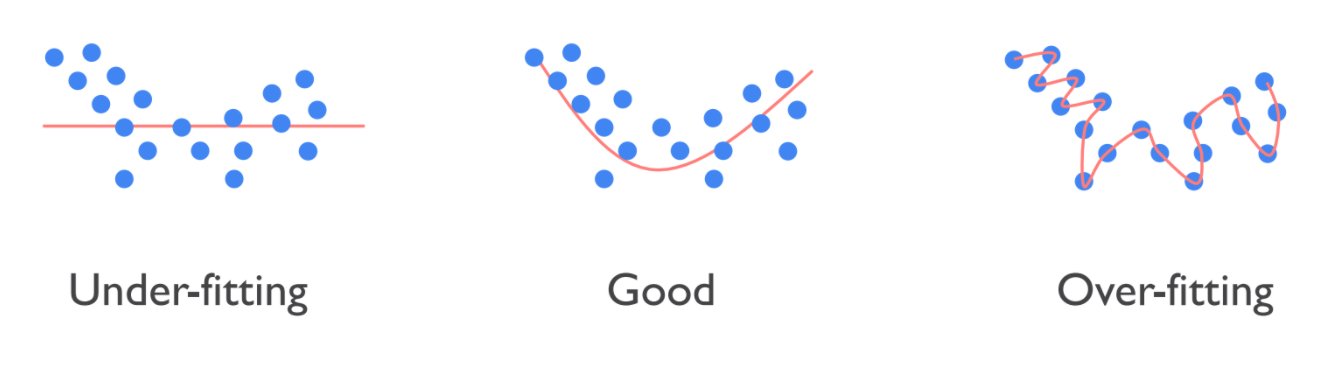
under over

Under-fitting is that trained model doesn't predict well on training dataset. Of course, it doesn't work well on test dataset, that may be unseen while training. We know that this is the problem we need to care. But the problem is also occurred in Over-fitting. Over-fitting is the situation that trained model works well on training dataset, but not work well on test dataset. That's because the model is not trained in terms of generalization. Many approaches can handle overfitting problem such as training model with larger dataset, and Dropout method is introduced here.

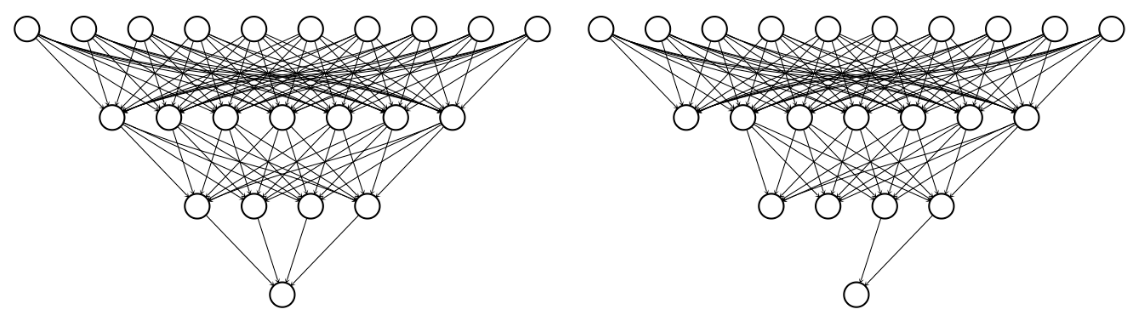
dropout

Previously, we just define the layer while we build the model. Instead of using whole nodes in layer, we can disable some nodes with some probability. For example, we can define drop rate of 50%, then we can use 50% of nodes in layers.

Thanks to Dropout, we can improve model performance in terms of generalization.

Code¶

Tensorflow implements Dropout layers for an API. So if you want to use, you can add it after each hidden layers like this,

for _ in range(2):
    # [N, 784] -> [N, 256] -> [N, 256]
    self.model.add(tf.keras.layers.Dense(256, use_bias=True, kernel_initializer=weight_init))
    self.model.add(tf.keras.layers.Activation(tf.keras.activations.relu))
    self.model.add(tf.keras.layers.Dropout(rate=0.5))

Batch Normalization¶

This section is related on the information distribution. If the distribution of input and output is normally distributed, the trained model may work well. But what if the distribution is crashed while information is pass through the hidden layer?

internal Covariate Shift

Even if the information in input layer distributed normally, mean and variance may be shifted and changed. This is called Internal Covariate Shift. To avoid this, what can we do?

If we remember the knowledge from statistics, there is a way to convert some distribution to unit normal distribution. Yes, it is Standardization. We can apply this and regenerate the distribution like this,

$$ \bar{x} = \frac{x - \mu_B}{\sqrt{\sigma_B^2 + \epsilon}} \qquad \hat{x} = \gamma \bar{x} + \beta $$

There is a noise term $\epsilon$, but it will make $\bar{x}$ to unit normal distribution (which has 0 mean and 1 variance). After adding $\gamma$ and $\beta$, we can make the distribution that we want to make.

Code¶

Tensorflow also implements BatchNormalization layers for an API. So if you want to use, you can add it after each hidden layers like this,

for _ in range(2):
    # [N, 784] -> [N, 256] -> [N, 256]
    self.model.add(tf.keras.layers.Dense(256, use_bias=True, kernel_initializer=weight_init))
    self.model.add(tf.keras.layers.BatchNormalization())
    self.model.add(tf.keras.layers.Activation(tf.keras.activations.relu))

Summary¶

In this post, we covered some techniques for improving neural network model, ReLU activation function, Weight Initialization, Dropout, and BatchNormalization.