10. Implementing QR Factorization¶

We used QR factorization in computing eigenvalues and to compute least squares regression. It is an important building block in numerical linear algebra.

"One algorithm in numerical linear algebra is more important than all the others: QR factorization." --Trefethen, page 48

Recall that for any matrix $A$, $A = QR$ where $Q$ is orthogonal and $R$ is upper-triangular.

Reminder: The QR algorithm, which we looked at in the last lesson, uses the QR decomposition, but don't confuse the two.

In Numpy¶

Check that Q is orthogonal:

Check that R is triangular

Linear Algebra Review: Projections¶

When vector $\mathbf{b}$ is projected onto a line $\mathbf{a}$, its projection $\mathbf{p}$ is the part of $\mathbf{b}$ along that line $\mathbf{a}$.

Let's look at interactive graphic (3.4) for section 3.2.2: Projections of the Immersive Linear Algebra online book.

(source: [Immersive Math](http://immersivemath.com/ila/ch03_dotproduct/ch03.html))

And here is what it looks like to project a vector onto a plane:

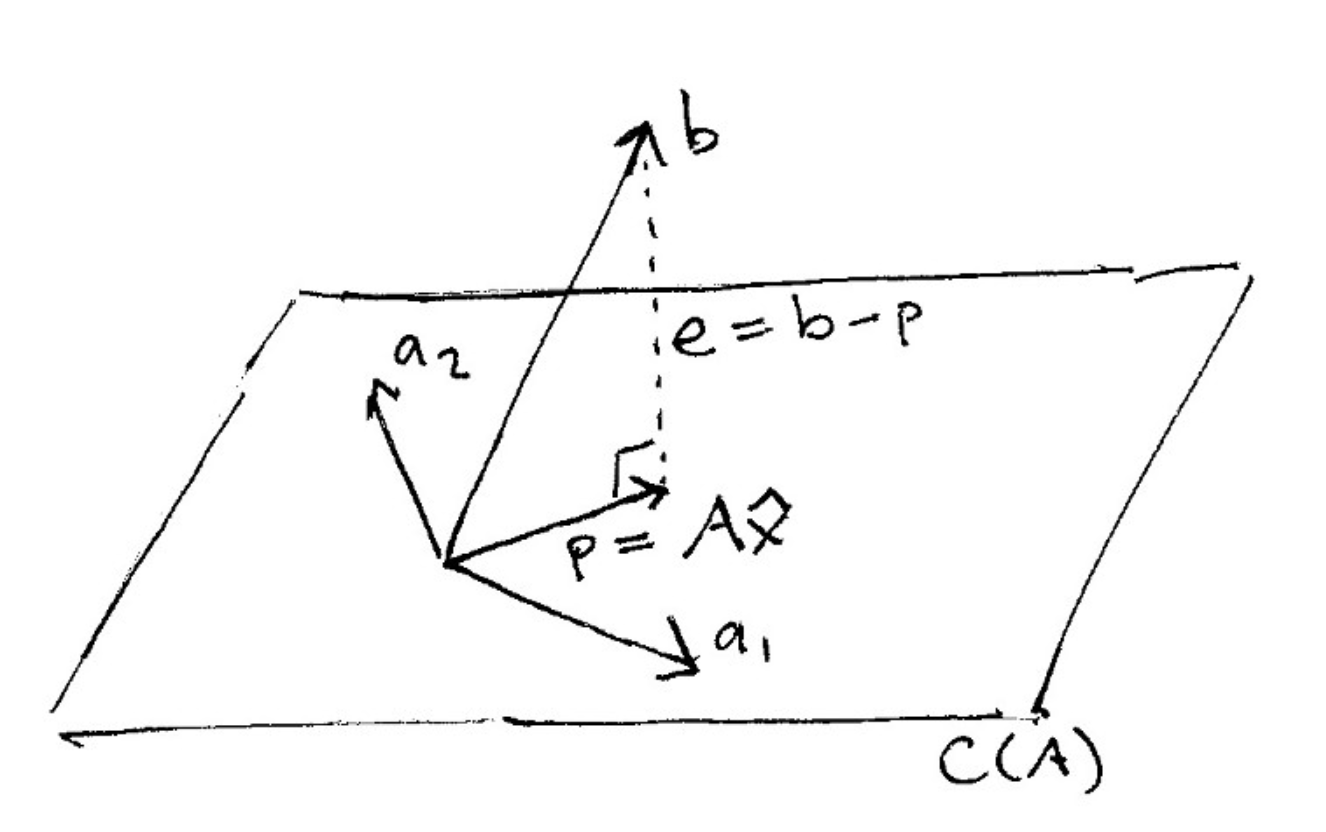(source: [The Linear Algebra View of Least-Squares Regression](https://medium.com/@andrew.chamberlain/the-linear-algebra-view-of-least-squares-regression-f67044b7f39b))

When vector $\mathbf{b}$ is projected onto a line $\mathbf{a}$, its projection $\mathbf{p}$ is the part of $\mathbf{b}$ along that line $\mathbf{a}$. So $\mathbf{p}$ is some multiple of $\mathbf{a}$. Let $\mathbf{p} = \hat{x}\mathbf{a}$ where $\hat{x}$ is a scalar.

Orthogonality¶

The key to projection is orthogonality: The line from $\mathbf{b}$ to $\mathbf{p}$ (which can be written $\mathbf{b} - \hat{x}\mathbf{a}$) is perpendicular to $\mathbf{a}$.

This means that $$ \mathbf{a} \cdot (\mathbf{b} - \hat{x}\mathbf{a}) = 0 $$

and so $$\hat{x} = \frac{\mathbf{a} \cdot \mathbf{b}}{\mathbf{a} \cdot \mathbf{a}} $$

Gram-Schmidt¶

Classical Gram-Schmidt (unstable)¶

For each $j$, calculate a single projection $$v_j = P_ja_j$$ where $P_j$ projects onto the space orthogonal to the span of $q_1,\ldots,q_{j-1}$.

Check if Q is unitary:

Gram-Schmidt should remind you a bit of the Arnoldi Iteration (used to transform a matrix to Hessenberg form) since it is also a structured orthogonalization.

Modified Gram-Schmidt¶

Classical (unstable) Gram-Schmidt: for each $j$, calculate a single projection $$v_j = P_ja_j$$ where $P_j$ projects onto the space orthogonal to the span of $q_1,\ldots,q_{j-1}$.

Modified Gram-Schmidt: for each $j$, calculate $j-1$ projections $$P_j = P_{\perp q_{j-1}\cdots\perp q_{2}\perp q_{1}}$$

Householder¶

Intro¶

\begin{array}{ l | l | c } \hline Gram-Schmidt & Triangular\, Orthogonalization & A R_1 R_2 \cdots R_n = Q \\ Householder & Orthogonal\, Triangularization & Q_n \cdots Q_2 Q_1 A = R \\ \hline \end{array}

Householder reflections lead to a more nearly orthogonal matrix Q with rounding errors

Gram-Schmidt can be stopped part-way, leaving a reduced QR of 1st n columns of A

Initialization¶

Algorithm¶

I added more computations and more info than needed, since it's illustrative of how the algorithm works. This version returns the Householder Reflectors as well.

Check that R is upper triangular:

As a check, we will calculate $Q^T$ and $R$ using the block matrices $F$. The matrices $F$ are the householder reflectors.

Note that this is not a computationally efficient way of working with $Q$. In most cases, you do not actually need $Q$. For instance, if you are using QR to solve least squares, you just need $Q^*b$.

• See page 74 of Trefethen for techniques to implicitly calculate the product $Q^*b$ or $Qx$.
• See these lecture notes for a different implementation of Householder that calculates Q simultaneously as part of R.

Here's a concise version of Householder (although I do create a new R, instead of overwriting A and computing it in place).

Check that R is diagonal:

Both classical and modified Gram-Schmidt require $2mn^2$ flops.

Gotchas¶

Some things to be careful about:

• when you've copied values vs. when you have two variables pointing to the same memory location
• the difference between a vector of length n and a 1 x n matrix (np.matmul deals with them differently)

Analogy¶

	$A = QR$	$A = QHQ^*$
orthogonal structuring	Householder	Householder
structured orthogonalization	Gram-Schmidt	Arnoldi

Gram-Schmidt and Arnoldi: succession of triangular operations, can be stopped part way and first $n$ columns are correct

Householder: succession of orthogoal operations. Leads to more nearly orthogonal A in presence of rounding errors.

Note that to compute a Hessenberg reduction $A = QHQ^*$, Householder reflectors are applied to two sides of A, rather than just one.

Examples¶

The following examples are taken from Lecture 9 of Trefethen and Bau, although translated from MATLAB into Python

Ex: Classical vs Modified Gram-Schmidt¶

This example is experiment 2 from section 9 of Trefethen. We want to construct a square matrix A with random singular vectors and widely varying singular values spaced by factors of 2 between $2^{-1}$ and $2^{-(n+1)}$

Ex: Numerical loss of orthogonality¶

This example is experiment 3 from section 9 of Trefethen.

Gram-Schmidt:

Householder:

Numpy's Householder:

Check that all the QR factorizations work:

Check how close Q is to being perfectly orthonormal:

GS (Q1) is less stable than Householder (Q2T, Q3)

End¶