Систематические ошибки¶
Из формулы для расчёта сечения для каждого её члена нужно выделить систематические ошибки $$\sigma = \frac{N_{sig}}{\varepsilon L (1+\delta)}$$
Известные ошибки:
| Вид систематики | Ошибка (%) |
|---|---|
| Ошибка светимости | 1 % |
| Точность формулы радпоправки | 0.5% |
Ошибки от критериев отбора событий¶
Я прочитал несколько презентаций по теме подсчёта систематик, где указано, что варьирование критериев отбора - это наивный и понятный, но не совсем корректный метод и совсем некорректный в случае малого количества сигнальных событий, т.к. статистические флуктуации сигнальных событий в варьируемой области сильно влияют на результат.
Предлагаются более изощрённые методы profile likelihood и т.п., но они мне пока непонятны, поэтому пользуюсь наивным подходом
Варьирую критерии отбора ($\pm 1\sigma$) и рассматриваю именение отношения $N_{sig}/\varepsilon_{reg}$ – число сигнальных событий к эффективности регистрации (*)
Поочерёдно варьирую критерии отбора (делается на примере данных 2011 года)
z-координата трека¶
Исходный кат |z| < 10 см. Выбирается грубо $\sigma_z$ = 1 см, смотрю как меняется отношение (*)
| Энергия пучка, МэВ | Сист.ошибка(%) |
|---|---|
| 525 | 0.06% |
| 800 | 0.57% |
| 900 | 0.01% |
Максимальная систематическая ошибка порядка 0.6%, что не является основным вкладом, как будет видно дальше и значит, можно перестать работать над оценкой влияния данного параметра
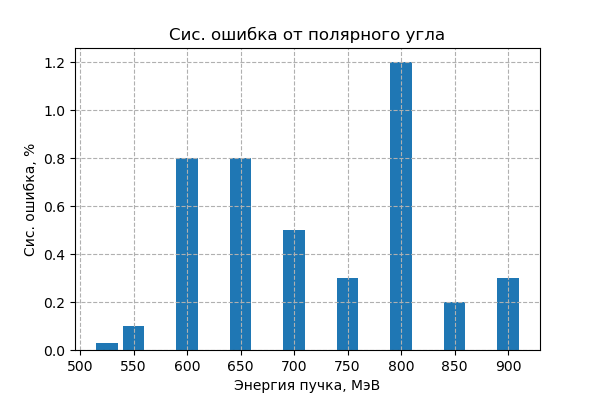
полярный угол $\theta$ трека¶
Исходный кат $0.6 < \theta < \pi - 0.6$
Выбирается $\sigma_{\theta} = 0.015$ (получен из разницы между генераторным и реконструированным значениями полярного угла в моделировании, что показано на рисунке снизу)
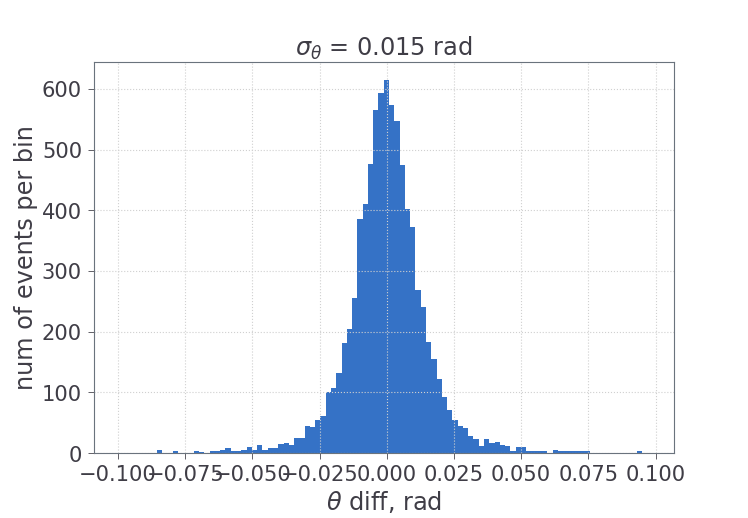
Изменение отношения (*) при варьировании критерия отбора по полярному углу на $\sigma_{\theta}$ в процентах (которое равно систематической ошибке) показано на рис. снизу
прицельный параметр трека¶
Исходный кат $|\rho| > 0.1$ см, т.к. заявленное разрешение дк составляет 120 мкм в $r-\phi$-плоскости, то беру $\sigma_{\rho}$ = 0.12 мм
В этом случае сист. ошибка
| Энергия пучка, МэВ | Сист.ошибка(%) |
|---|---|
| 525 | 0.46% |
| 800 | 0.05% |
| 900 | 1% |
ионизационные потери трека¶
Исходный кат $|f(P_{track}, dE/dX)| < 2000$
Предполагая, что в идеальном случае распределение событий по ионизационным потерям пионов в зависимости от импульсов их треков лежало бы "строго" на кривой $f(P_{track}, dE/dX) = 0$, можно определить разрешение по данному параметру из моделирования. $\sigma_{dEdX} = 500$
Варьирование $\pm 1 \sigma_{dEdX}$ приводит к следующему вкладу в сист. ошибку

Вклад в систематическую ошибку для энергии 900 МэВ составил 11%. В этом случае и при энергии 850 МэВ как раз ярко виден недостаток данного метода, когда статистическая флуктуация в 1 событие кардинально влияет на результат (хотя с точки зрения статистики данная флуктуация вписывается в сигму)
отбор по косинусу угла отлёта¶
Исходный кат $\cos{\alpha} < 0.8$. Разрешение по $\alpha$ бралось таким же как для $\theta$, т.о. $\sigma_\alpha = 0.015$
В этом случае сист. ошибка
| Энергия пучка, МэВ | Сист.ошибка(%) |
|---|---|
| 525 | 0.03% |
| 550 | 0.06% |
| 800 | 0.03% |
| 900 | 0% |
не вносит заметного вклада, поэтому может не рассматриваться в дальнейшем
отбор по инв.массе/импульсу каонов¶
Исходный кат $g(P[K], M_{inv}[K]) < 10$ МэВ. Для напоминания распределение событий по инв.массе KS в зависимости от его импульса и критерий отбора показаны на рис. снизу

В идеальном случае здесь должна была получаться точка с координатами (P_0, 497.6), поэтому стандартное отклонение в отобранной области будет характеризовать разрешение по данному параметру, которое получилось равно $\sigma_{MP} = 4$ МэВ
Варьирование $\pm \sigma_{MP}$ приводит ко вкладу в систематику от данного отбора, представленному на рисунке снизу
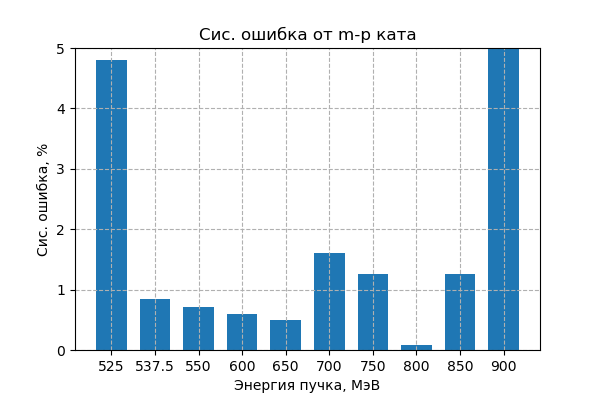
Снова ошибка на энергии 900 МэВ зашкаливает и равна 14%, и снова из-за небольшой статистической флуктуации при малом общем количестве событий
Интересное значение у систематической ошибки при энергии 525 МэВ, где она составляет 4.8%. Это можно связать с присутствующим рядом $\phi$-мезоном, на который активно идёт сброс. Кат режет по живому в данном случае.
итоговая систематика от критериев отбора¶
Таким образом, каты проверены, теперь нужно определить полный вклад в систематику от критериев отбора. Я не буду складывать квадратичным образом систематики от каждого критерия, поскольку они друг с другом скоррелированы, поэтому по итогу я проварьирую вместе критерии по $\theta$, $dE/dX$ и инв.массе/импульсу каонов, т.к. эти критерии дают сопоставимый вклад, и итоговое изменение отношения (*) будет характеризовать полный вклад в систематику от критериев отбора
В результате систематическая ошибкаот критериев отбора по энергиям показана на рис. снизу
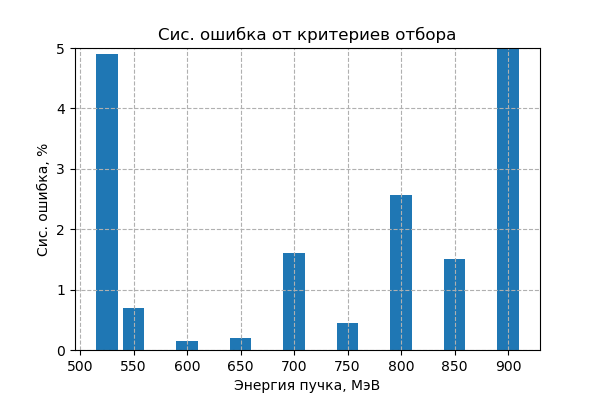
В точке 525 МэВ основная систематика из отбора по инв.массе/импульсу каонов, поэтому конкретно для этой точки можно попробовать его переработать, чтоб уменьшить ошибку
В точке 900 МэВ систематика составила 14%, я считаю это проблемой метода (т.к. в этой точке при стандартных критериях отбора наблюдается 2 сигнальных события и любая флуктуация в относительном масштабе огромна).
По факту, во всех точках, даже 525 МэВ, наблюдается та же проблема, и флуктуация числа событий в эксперименте при варьировании критериев отбора сравнима с флуктуацией случайной величины, что говорит о том, что метод возможно некорректен во всех случаях
Например, вариация ката по $dE/dX$ в точке с энергией 550 МэВ. Получены результаты, представленные на рис. снизу

Видно, что то, что называется систематической ошибкой, здесь всего лишь может быть проинтерпретировано как флуктуация случайной величины (вполне небезосновательно)
Таким образом, полученный результат ставится под сомнение