from IPython.core.display import HTML, Image
from IPython.display import YouTubeVideo
from sympy import init_printing, Matrix, symbols, Rational
import sympy as sym
from warnings import filterwarnings
init_printing(use_latex = 'mathjax')
filterwarnings('ignore')
%pylab inline
import numpy as np
Populating the interactive namespace from numpy and matplotlib
Some important notes¶
- HW1 is out! Due January 25th at 11pm
- Homework will be submitted via Gradescope. Please see Piazza for precise instructions. Do it soon, not at the last minute!!
- There is an optional tutorial this evening, 5pm, in Dow 1013. Come see Daniel go over some tough problems.
- No class on Monday January 18, MLK day!
Python: We recommend Anacdona¶
 * Anaconda is standalone Python distribution that includes all the most important scientific packages: *numpy, scipy, matplotlib, sympy, sklearn, etc.*
* Easy to install, available for OS X, Windows, Linux.
* Small warning: it's kind of large (250MB)
* Anaconda is standalone Python distribution that includes all the most important scientific packages: *numpy, scipy, matplotlib, sympy, sklearn, etc.*
* Easy to install, available for OS X, Windows, Linux.
* Small warning: it's kind of large (250MB)
Some notes on using Python¶
- HW1 has only a very simple programming exercise, just as a warmup. We don't expect you to submit code this time
- This is a good time to start learning Python basics
- There are a ton of good places on the web to learn python, we'll post some
- Highly recommended: ipython; it's a much more user friendly terminal interface to python
- Even better: jupyter notebook, a web based interface. This is how I'm making these slides!
Checking if all is installed, and HelloWorld¶
If you got everything installed, this should run:
# numpy is crucial for vectors, matrices, etc.
import numpy as np
# Lots of cool plotting tools with matplotlib
import matplotlib.pyplot as plt
# For later: scipy has a ton of stats tools
import scipy as sp
# For later: sklearn has many standard ML algs
import sklearn
# Here we go!
print("Hello World!")
More on learning python¶
- We will have one tutorial devoted to this
- If you're new to Python, go slow!
- First learn the basics (lists, dicts, for loops, etc.)
- Then spend a couple days playing with numpy
- Then explore matplotlib
- etc.
- Piazza = your friend. We have a designated python instructor (IA Ben Bray) who has lots of answers.
Outline for this Lecture¶
- Convexity
- Convex Set
- Convex Function
- Introduction to Optimization
- Introduction to Lagrange Duality
In this lecture, we will first introduce convex set, convex function and optimization problem. One approach to solve optimization problem is to solve its dual problem. We will briefly cover some basics of duality in this lecture. More about optimization and duality will come when we study support vector machine (SVM).
Convex Functions¶
- We say that a function $f$ is convex if, for any distinct pair of points $x,y$ we have
- A function $f$ is said to be concave if $-f$ is convex
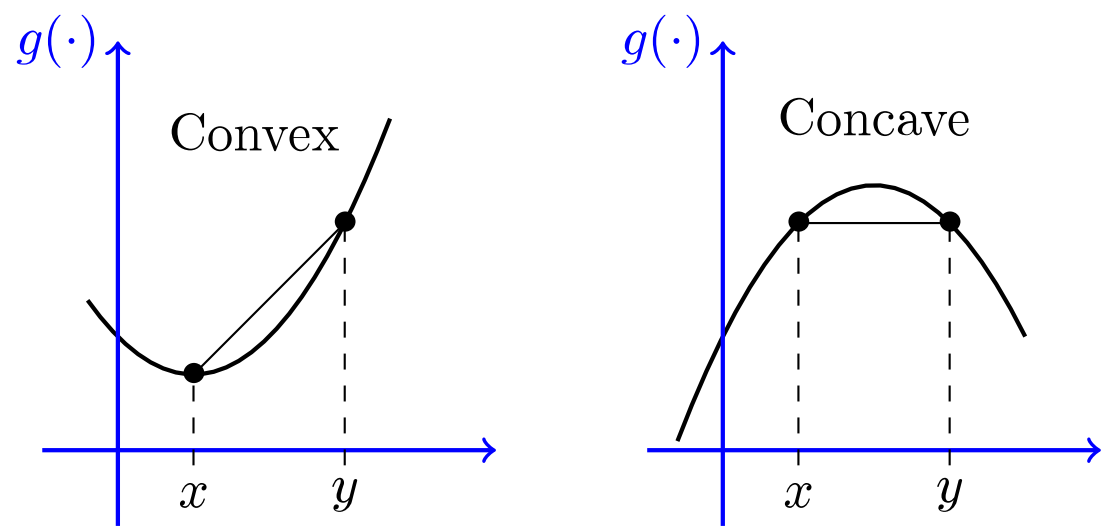
Fun Facts About Convex Functions¶
- If $f$ is differentiable, then $f$ is convex iff $f$ "lies above its linear approximation", i.e.:
- If $f$ is twice-differentiable, then the hessian is always positive semi-definite!
- This last one you will show on your homeowork :-)
Introduction to Optimization¶
The Most General Optimization Problem¶
Assume $f$ is some function, and $C \subset \mathbb{R}^n$ is some set. The following is an optimization problem: $$ \begin{array}{ll} \mbox{minimize} & f(x) \\ \mbox{subject to} & x \in C \end{array} $$
- How hard is it to find a solution that is (near-) optimal? This is one of the fundamental problems in Computer Science and Operations Research.
- A huge portion of ML relies on this task
A Rough Optimization Hierarchy¶
$$ \mbox{minimize } \ f(x) \quad \mbox{subject to } x \in C $$- [Really Easy] $C = \mathbb{R}^n$ (i.e. problem is unconstrained), $f$ is convex, $f$ is differentiable, strictly convex, and "slowly-changing" gradients
- [Easyish] $C = \mathbb{R}^n$, $f$ is convex
- [Medium] $C$ is a convex set, $f$ is convex
- [Hard] $C$ is a convex set, $f$ is non-convex
- [REALLY Hard] $C$ is an arbitrary set, $f$ is non-convex
Optimization Without Constraints¶
$$ \begin{array}{ll} \mbox{minimize} & f(x) \\ \mbox{subject to} & x \in \mathbb{R}^n \end{array} $$- This problem tends to be easier than constrained optimization
- We just need to find an $x$ such that $\nabla f(x) = \vec{0}$
- Techniques like gradient descent or Newton's method work in this setting. (More on this later)
Optimization With Constraints¶
$$ \begin{aligned} & {\text{minimize}} & & f(\mathbf{x})\\ & \text{subject to} & & g_i(\mathbf{x}) \leq 0, \quad i = 1, ..., m\\ & & & h_j(x) = 0, \quad j = 1, ..., n \end{aligned} $$- Here $C = \{ x : g_i(x) \leq 0,\ h_j(x) = 0, \ i=1, \ldots, m,\ j = 1, ..., n \}$
- $C$ is convex as long as all $g_i(x)$ convex and all $h_j(x)$ affine
- The solution of this optimization may occur in the interior of $C$, in which case the optimal $x$ will have $\nabla f(x) = 0$
- But what if the solution occurs on the boundary of $C$?

Introduction to Lagrange Duality¶
- In some cases original (primal) optimization problem can hard to solve, solving a proxy problem sometimes can be easier
- The proxy problem could be dual problem which is transformed from primal problem
- Here is how to transform from primal to dual. For primal problem
Its Lagrangian is $$L(x,\boldsymbol{\lambda}, \boldsymbol{\nu}) := f(x) + \sum_{i=1}^m \lambda_i g_i(x) + \sum_{j=1}^n \nu_j h_j(x)$$ of which $\boldsymbol{\lambda} \in \mathbb{R}^m$, $\boldsymbol{\nu} \in \mathbb{R}^n$ are dual variables
- The Langragian dual function is
The minization is usually done by finding the stable point of $L(x,\boldsymbol{\lambda}, \boldsymbol{\nu})$ with respect to $x$
The Lagrange Dual Problem¶
- Then the dual problem is
Instead of solving primal problem with respect to $x$, we now need to solve dual problem with respect to $\mathbf{\lambda}$ and $\mathbf{\nu}$
- $ L_D(\mathbf{\lambda}, \mathbf{\nu})$ is concave even if primal problem is not convex
- Let the $p^*$ and $d^*$ denote the optimal values of primal problem and dual problem, we always have weak duality: $p^* \geq d^*$
- Under nice conditions, we get strong duality: $p^* = d^*$
- Many details are ommited here and they will come when we study support vector machine (SVM)


