from IPython.display import HTML
HTML("""<center>
<iframe width="560" height="315" src="https://www.youtube-nocookie.com/embed/U3nGNJTxYc4?rel=0" frameborder="0" allow="accelerometer; autoplay; clipboard-write; encrypted-media; gyroscope; picture-in-picture" allowfullscreen></iframe>
</center>""")
La récursivité est donc une méthode de résolution de problèmes qui consiste à décomposer le problème en sous-problèmes identiques de plus en plus petits jusqu’à obtenir un problème suffisamment petit pour qu’il puisse être résolu de manière triviale.

Exemple :¶
Étant donné une liste d’entiers L=[2,12,1,8,5,10,20], calculer la somme des éléments de cette liste.
Comme les listes sont itérables, nous pouvons simplement résoudre ce problème avec l’un ou l'autre de ces algorithmes que l’on dit itératifs :
pseudo
Données : liste ← une liste d’entiers
fonction somme_1(liste)
S ← 0
n ← longueur de la liste
Pour i allant de 0 à n faire
S ← S + liste[i]
renvoyer S
OU
pseudo
Données : liste ← une liste d’entiers
fonction somme_2(liste)
S ← 0
Pour chaque element de liste faire
S ← S + element
renvoyer S
OU
pseudo
Données : liste ← une liste d’entiers
fonction somme_3(liste)
S ← 0
i ← 0
Tant que i < longueur de la liste
S ← S + liste[i]
i ← i + 1
renvoyer S
A faire vous même n°2 :
- Pour vous échauffer, implémenter en Python ces trois algorithmes itératifs et tester les :
assert somme([2,12,1,8,5,10,20]) == 58, "Test non concluant !"
print("Test concluant !")
Supposons maintenant que nous n’ayons pas la possibilité de faire de "boucles".
On peut alors aborder le problème sous un autre angle :
La somme des termes de cette liste est: 2 + ( la somme des termes de [12,1,8,5,10,20])
Soit : 2 + (12 + (la somme des termes de [1,8,5,10,20])
et ainsi de suite... jusqu’à : 2 + (12 + (1 + (8 + (5 + (10 + ( la somme des termes de [20]))))))
il est clair que : la somme des termes de [20] est 20
Au final le calcul à faire est : 2 + (12 + (1 + (8 + (5 + (10 + (20)))))) = 58
Considérons alors une fonction sommeliste(liste) et qui renvoie le résultat de la somme des éléments de la liste.
L’algorithme ci-dessous que l’on dit récursif réalise cette seconde approche:
pseudo
Données : liste ← une liste d’entiers
fonction sommeliste(liste)
Si la longueur de la liste est égale à 1 alors
renvoyer liste[0]
Sinon
renvoyer liste[0] + sommeliste(liste[1:])
A faire vous même n°3 :
- Implémenter en Python cette fonction et la tester également :
assert sommeliste([2,12,1,8,5,10,20]) == 58, "Test non concluant"
print("Test concluant !")
A faire vous même n°4 :
- Comparer les vitesses d’exécutions des programmes version itérative et version récursive de l’exemple précédent.
Pour tester la vitesse d’exécution d’une fonction on utilise le module timeit, comme le montre le code ci-dessous pour une liste de 1000 entiers choisis aléatoirement entre 0 et 100 avec le module random.
from timeit import default_timer as timer
from random import randint
# Ajouter les codes des deux fonctions à comparer ici
L=[randint(0,100) for i in range(1000)]
debut = timer()
print(sommeliste(L))
fin = timer()
print(fin-debut)
debut = timer()
print(somme(L))
fin = timer()
print(fin - debut)
- Que pouvez-vous en conclure (pour cet exemple)?
...
Complexité et fonctionnement d'un programme récursif :¶
A faire vous même n°5 :
- Observer le fonctionnement des appels récursifs de la fonction
sommeliste(liste)dans votre programme avec l'outil Python tutor permet de visualiser pas à pas ce que fait votre script.
Il est possible de l'utiliser dans un notebook jupyter (mais hors Capytale) pour celà il faut :
> 1. l'installer (si ce n'est pas déjà fait) : ``%pip install metakernel``
> 1. puis exécuter les instructions de la cellule suivante :
from metakernel import register_ipython_magics
register_ipython_magics()
>3. inscrire la commande ``%%tutor`` devant le script à tester dans la cellule :
%%tutor
# Script à tester :
# Ajouter le code de votre fonction sommeliste(liste) ici
print(sommeliste([2,12,1,8,5,10,20]))
Un programme est une suite d’instructions, son exécution peut être représentée par un parcours de chemin ayant une origine et une extrémité.
Lors de l’appel d’une fonction, cette suite est interrompue le temps de cette fonction, avant de reprendre à l’endroit où le programme s’est arrêté.
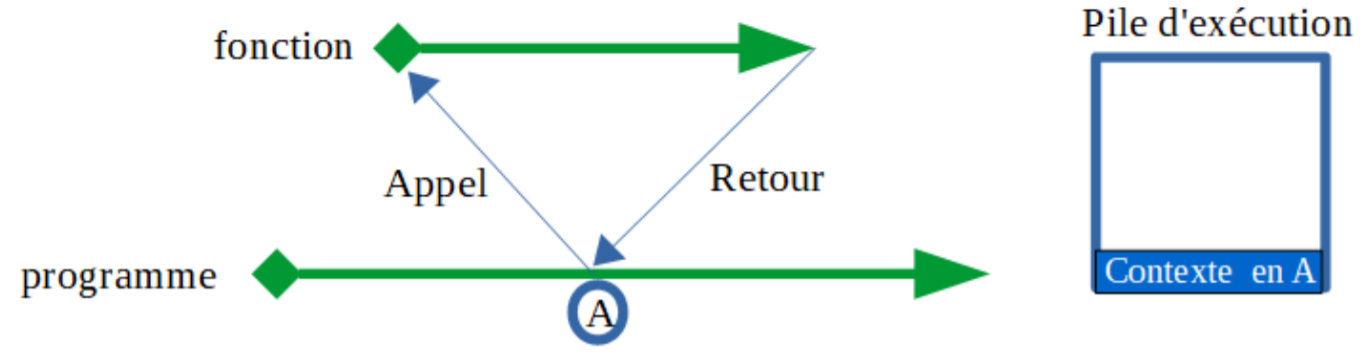
Au moment où débute cette bifurcation, le processeur sauvegarde un certain nombre d’informations : adresse de retour, état des variables, etc.
Toutes ces données forment ce qu’on appelle le contexte du programme, et elles sont stockées dans ce qu’on appelle la pile d’exécution.
À la fin de l’exécution de la fonction, le contexte est sorti pour permettre la poursuite de l’exécution du programme.
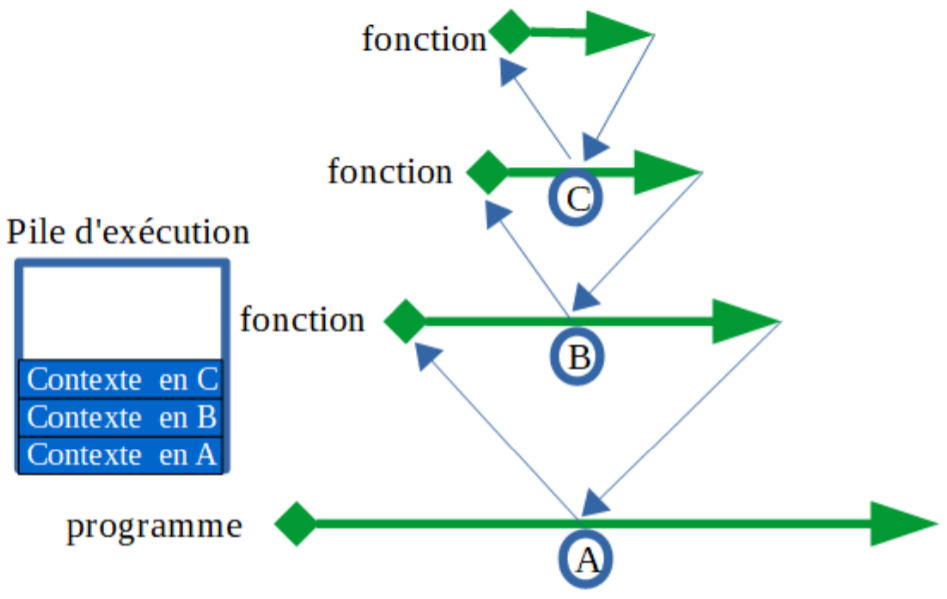
Lors de l’exécution d’une fonction récursive, chaque appel récursif conduit, au moment où il se produit, à un empilement du contexte dans la pile d’exécution.
Lorsqu’au bout de n appels se produit la condition d’arrêt, les différents contextes sont progressivement dépilés pour poursuivre l’exécution de la fonction.
Il est important de prendre conscience qu’une fonction récursive s’accompagne d’une complexité qui va croître avec le nombre d’appels récursifs (en général linéairement, mais ce n’est pas une règle, cela dépend du contenu du contexte).
Les trois règles...¶
A l'instar des robots d’Azimov, les algorithmes récursifs doivent obéir à trois règles :
- Un algorithme récursif doit avoir un " état trivial ", cela permet d’avoir une condition d’arrêt.
Dans notre exemple, il s’agit de : si la liste est de longueur 1 alors on renvoie le seul élément de la liste.
- Un algorithme récursif doit conduire vers cet " état d’arrêt ", cela permet de ne pas faire une infinité d’appels récursifs.
Dans notre exemple, à chaque appel récursif, la liste est diminuée d’un élément donc nécessairement elle finira par n’en n’avoir plus qu’un.
- Un algorithme récursif s’appelle lui même...
Itératif vs Récursif¶
Il n’existe pas de réponse définitive à la question de savoir si un algorithme récursif est préférable à un algorithme itératif ou le contraire.
Il a été prouvé que ces deux paradigmes de programmation sont équivalents ; autrement dit, tout algorithme itératif possède une version récursive, et réciproquement.
Le choix du langage peut aussi avoir son importance : un langage fonctionnel est conçu pour exploiter la récursivité et le programmeur est naturellement amené à choisir la version récursive de l’algorithme qu’il souhaite écrire.
À l’inverse, Python, même s’il l’autorise, ne favorise pas l’écriture récursive (limitation basse (1000 par défaut) du nombre d’appels récursifs).
Enfin, le choix d’écrire une fonction récursive ou itérative peut dépendre du problème à résoudre : certains problèmes se résolvent particulièrement simplement sous forme récursive.
Application 1 : version récursive du convertisseur...
Petit rappel :¶
Une méthode de conversion consiste à diviser le nombre décimal à convertir par la base b et conserver le reste de la division. Le quotient obtenu est divisé par b et conserver le reste. Il faut répéter l’opération sur chaque quotient obtenu.
Par exemple, pour la conversion : $91$ = $01011011_2$

Les restes successifs sont écrits, en commençant par le dernier, de la gauche vers la droite. Cette méthode est dite « Méthode des divisions successives ».
Voici un programme itératif qui réalise ce changement de base :
def decTob(n,b):
assert (b > 1 and b < 17) , "b doit être compris entre 2 et 16"
signes = ["0","1","2","3","4","5","6","7","8","9","A","B","C","D","E","F"]
mot = ""
while n != 0:
mot = signes[n % b] + mot
n = n // b
return mot
Analysons ce programme :
- La première ligne permet de s’assurer que les conditions sur b sont assurées ;
- La liste signes nous permet d’avoir accès aux symboles représentant les nombres jusqu’à la base 16 ;
- On utilisera la variable mot de type str pour le résultat ;
- Tant que n != 0 (tant que le quotient n’est pas nul), on ajoute par la gauche le reste au résultat et on remplace n par le nouveau quotient n // b.
A faire vous même n°6 :
- Tester ce programme avec différentes bases pour vérifier que vous obtenez les mêmes résultats qu'avec :
print(bin(77)[2:]) ## affiche 77 en base 2
print(oct(77)[2:]) ## affiche 77 en base 8
print(hex(77)[2:]) ## affiche 77 en base 16
Recherchons maintenant une version récursive de ce programme.
L’idée est :
decTobr(n, b) = decTobr(n // b, b) + reste
Pour ce faire suivons les trois règles :
Un algorithme récursif doit avoir un "état trivial", cela permet d’avoir une condition d’arrêt.
Un algorithme récursif doit conduire vers cet "état d’arrêt", cela permet de ne pas faire une infinité d’appels récursifs.
Un algorithme récursif s’appelle lui même...
A faire vous même n°7 :
- Répondre aux questions :
Q1) Dans notre cas quel est "l’état trivial" ?
...
Q2) Expliquer ce qui va conduire à cet "état trivial" ?
...
...
...
- Réaliser une version récursive du programme précédent :
Application 2 : Calculer le factoriel d'un nombre :
Écrire les versions itérative et récursive de fonctions calculant $n!$ où ${n\in\mathbf{N}}$ ;
sachant que : $n! = n × (n − 1) × (n − 2) × ... × 2 × 1 $ ;
et que par définition $0! = 1$.
Références aux programmes :¶
Langages et programmation
| Contenus | Capacités attendues | Commentaires |
|---|---|---|
| Récursivité. | Écrire un programme récursif. Analyser le fonctionnement d’un programme récursif. |
Des exemples relevant de domaines variés sont à privilégier. |

Ce document, basé sur le travail de Stephan VAN ZUIJLEN, est mis à disposition selon les termes de la Licence Creative Commons Attribution - Partage dans les Mêmes Conditions 4.0 International.
Pour toute question, suggestion ou commentaire : eric.madec@ecmorlaix.fr